Exam 6: Additional Topics In Trigonometery
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Use DeMoivre's Theorem to find the indicated power of the complex number.Write the result in standard form.
(Multiple Choice)
4.7/5  (36)
(36)
Determine the area of a triangle having the following measurements.Round your answer to two decimal places. C = 73 , a = 12.5 and b = 11.5
(Multiple Choice)
5.0/5  (28)
(28)
Select the graph of all complex numbers z satisfying the given condition.
(Multiple Choice)
4.8/5  (33)
(33)
Find the component form of v if and the angle it makes with the x-axis is 150°.
(Multiple Choice)
4.7/5  (31)
(31)
Use the vectors , and to find the indicated quantity.State whether the result is a vector or a scalar.
(Multiple Choice)
4.8/5  (31)
(31)
Determine whether u are v and orthogonal, parallel, or neither.
(Multiple Choice)
4.9/5  (39)
(39)
Find the product using trigonometric forms.Leave the result in trigonometric form.
(Multiple Choice)
4.8/5  (38)
(38)
Given vectors , and determine whether the result of the following expression is a vector or a scalar.
(Multiple Choice)
4.8/5  (31)
(31)
Perform the operation and leave the result in trigonometric form.
(Multiple Choice)
4.8/5  (31)
(31)
Given a = 7, b = 10, and c = 11, use the Law of Cosines to solve the triangle for the value of С.Round your answer to two decimal places. 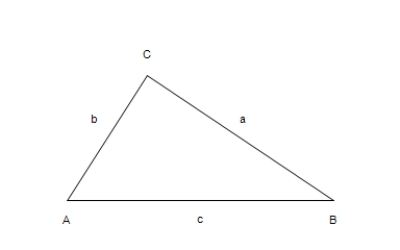 Figure not drawn to scale
Figure not drawn to scale
(Multiple Choice)
4.9/5  (34)
(34)
Given a = 9, b = 13, and c = 8, use the Law of Cosines to solve the triangle for the value of A.Round your answer to two decimal places. 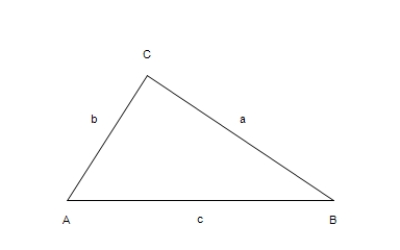 Figure not drawn to scale
Figure not drawn to scale
(Multiple Choice)
4.8/5  (49)
(49)
Find values for b such that the triangle has no solutions.
A = 54°, a = 19
(Multiple Choice)
4.9/5  (28)
(28)
Given a = 10, b = 12, and c = 8, use the Law of Cosines to solve the triangle for the value of B.Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (36)
(36)
A force of pounds exerted at an angle of above the horizontal is required to slide a table across a floor (see figure).The table is dragged feet.Determine the work done in sliding the table. 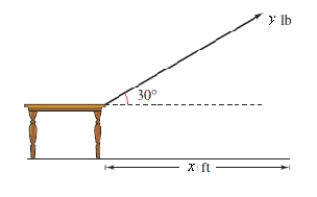
(Multiple Choice)
4.8/5  (28)
(28)
Showing 21 - 40 of 304
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)