Exam 9: Sequences Series and Probability
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
You are given the probability that an event will happen.Find the probability that the event will not happen.
(Multiple Choice)
4.8/5  (33)
(33)
Write the first five terms of the sequence.Determine whether the sequence is arithmetic.If so, find the common difference.(Assume that n begins with 1.)
An = 135 - 5n
(Multiple Choice)
5.0/5  (24)
(24)
You are given the probability that an event will not happen.Find the probability that the event will happen.
(Multiple Choice)
4.8/5  (42)
(42)
Write the first five terms of the arithmetic sequence.
A1 = 5, d = 7
(Multiple Choice)
4.7/5  (36)
(36)
Ten people are boarding an aircraft.Two have tickets for first class and board before those in the economy class.In how many ways can the ten people board the aircraft?
(Multiple Choice)
4.8/5  (36)
(36)
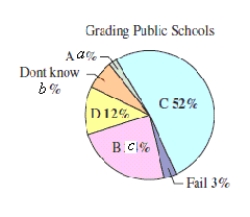
The figure shows the results of a recent survey in which 1011 adults were asked to grade U.S.public schools.An adult is selected at random.What is the probability that the adult will give the U.S.public schools an A
( , , ) 
(Multiple Choice)
4.7/5  (42)
(42)
Determine the number of ways a computer can randomly generate two distinct integers whose sum is 13 from 1 through 17 in increasing order.
(Multiple Choice)
4.9/5  (38)
(38)
Use the Binomial Theorem to expand and simplify the expression.
(Multiple Choice)
4.7/5  (45)
(45)
Find the probability for the experiment of selecting one card from a standard deck of 52 playing cards.
The card is a 7 or lower.(Aces are low.)
(Multiple Choice)
4.9/5  (38)
(38)
Use the Binomial Theorem to expand and simplify the expression.
(Multiple Choice)
4.9/5  (37)
(37)
Write the first six terms of the sequence beginning with the given term.Then calculate the first and second differences of the sequence.State whether the sequence has a linear model, a quadratic model, or neither.
A1 = 0
An = an - 1 + 5
(Multiple Choice)
4.9/5  (43)
(43)
You are given the probability that an event will happen.Find the probability that the event will not happen.
(Multiple Choice)
4.8/5  (43)
(43)
Find the sum of the indicated terms of the geometric sequence.
(Multiple Choice)
4.9/5  (35)
(35)
You are given the probability that an event will happen.Find the probability that the event will not happen.
(Multiple Choice)
4.8/5  (34)
(34)
Use a graphing utility to graph the first 10 terms of the sequence.(Assume that n begins with 1.) You may need to adjust the graphing window to the sizes indicated below to answer the question.
an = -0.4n + 12
(Multiple Choice)
4.9/5  (35)
(35)
Select the first five terms of the sequence.(Assume that n begins with 1.)
(Multiple Choice)
4.7/5  (40)
(40)
Showing 381 - 400 of 405
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)