Exam 13: Indefinite Integrals
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
If consumption C is $1 billion when disposable income y is 0, and if the marginal propensity to consume is 0.60, find the national consumption function C as a function of y (in billions of dollars). Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
If consumption is $8 billion when disposable income is 0, and if the marginal propensity to consume is 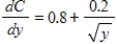 (in billions of dollars), find the national consumption function. If it's necessary, round your answer to two decimal places.
(in billions of dollars), find the national consumption function. If it's necessary, round your answer to two decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Suppose that a liquid carries a drug into a 400-cc organ at a rate of 20 cc/s and leaves the organ at the same rate. Suppose that the concentration of the drug entering is 0.25 g/cc. Find the amount A of drug in the organ as a function of time t if initially there is none in the organ. If it's necessary, round your calculations to four decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
A certain radioactive substance has a half-life of 75 hours. Find how long it will take, to the nearest hour, for 75% of the radioactivity to be dissipated if the amount of material x satisfies 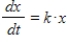 (t in hours). Round your answer to the nearest hour.
(t in hours). Round your answer to the nearest hour.
(Multiple Choice)
4.9/5  (47)
(47)
Suppose that a particle has been shot into the air in such a way that the rate at which its height H (in feet per second) is changing is 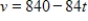 . If the particle is 4,200 feet high when
. If the particle is 4,200 feet high when 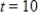 seconds, write the formula for the height of the particle at any time t.
seconds, write the formula for the height of the particle at any time t.
(Multiple Choice)
4.8/5  (40)
(40)
Suppose an oil tanker hits a reef and begins to leak. The efforts of the workers repairing the leak cause the rate at which the oil is leaking to decrease. The oil was leaking at a rate of 41 barrels per hour at the end of the first hour after the accident, and the rate is decreasing at a rate of one barrel per hour. What formula describes the rate of loss in terms of the time t that has lapsed since the leak began?
(Multiple Choice)
4.7/5  (33)
(33)
Suppose that the marginal revenue for a product is 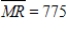 and the marginal cost is
and the marginal cost is 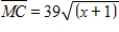 , with a fixed cost of
, with a fixed cost of 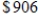 . Find the profit or loss from the production and sale of 3 units.
. Find the profit or loss from the production and sale of 3 units.
(Multiple Choice)
4.8/5  (34)
(34)
When the interest on an investment is compounded continuously, the investment grows at a rate that is proportional to the amount in the account. If $25,000 is invested (when 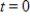 ) and the amount in the account after 18 years is $46,940.26, find the interest rate on this investment? Round to one decimal place.
) and the amount in the account after 18 years is $46,940.26, find the interest rate on this investment? Round to one decimal place.
(Multiple Choice)
4.7/5  (31)
(31)
Suppose that the marginal cost for a certain product is given by 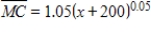 , where x is in thousand of units and cost is in thousands of dollars. Suppose further that fixed costs are $210,000. Find
, where x is in thousand of units and cost is in thousands of dollars. Suppose further that fixed costs are $210,000. Find 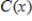 . Round your answer to three decimal places, if necessary.
. Round your answer to three decimal places, if necessary.
(Multiple Choice)
4.8/5  (33)
(33)
Because of job outsourcing, a western Pennsylvania town predicts that its public school population will decrease at the rate 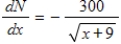 , where x is the number of years and N is the total school population. If N = 7,800 when x = 0, what population size is expected in 6 years? Round your answer to nearest integer when applicable.
, where x is the number of years and N is the total school population. If N = 7,800 when x = 0, what population size is expected in 6 years? Round your answer to nearest integer when applicable.
(Multiple Choice)
4.8/5  (34)
(34)
Find the particular solution to the differential equation 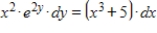 that satisfies
that satisfies 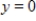 when
when 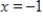 .
.
(Multiple Choice)
4.9/5  (35)
(35)
The impact of inflation on a fixed pension can be severe. If P represents the purchasing power (in dollars) of a $50,000 pension, then the effect of a 2.5% inflation rate can be modeled by the differential equation 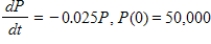 , where t is in years. Find the purchasing power of the pension after 35 years. Round to the nearest dollar.
, where t is in years. Find the purchasing power of the pension after 35 years. Round to the nearest dollar.
(Multiple Choice)
4.9/5  (34)
(34)
Use integration to find the general solution to the differential equation 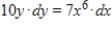 .
.
(Multiple Choice)
4.8/5  (43)
(43)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)