Exam 7: Scatterplots, Association, and Correlation
Exam 1: Stats Start Here115 Questions
Exam 2: Data150 Questions
Exam 3: Displaying and Describing Categorical Data110 Questions
Exam 4: Displaying and Comparing Qualitative Data84 Questions
Exam 5: Understanding and Comparing Distributions103 Questions
Exam 6: The Standard Deviation As a Ruler and the Normal Model74 Questions
Exam 7: Scatterplots, Association, and Correlation40 Questions
Select questions type
For the scenario described below, simply name the procedure that is appropriate to answer the question. For example,
1-proportion z-interval or chi-square goodness of fit test. Do NOT carry out the procedure.
-In a campus survey, a university polls its students to see how many hours they study in an average week. Females reported an average of 16.8 hours, while males reported an average of 13.8 hours. Find a 95% confidence interval for the difference in average time spent studying by females compared to males.
(Short Answer)
4.9/5  (26)
(26)
A college admissions counselor was interested in finding out how well high school grade point averages (HS GPA) predict first-year college GPAs (FY GPA). A random sample of data from first-year students was reviewed to obtain high school and first-year college GPAs. The data are shown below:
HS GPA 3.82 3.90 3.20 3.40 3.88 3.50 3.60 3.70 FY GPA 3.75 3.45 2.60 2.95 3.50 2.76 3.10 3.40
HS GPA 4.00 3.30 3.50 3.80 3.87 4.00 3.20 3.82 FY GPA 3.90 2.70 3.00 3.00 3.10 3.77 2.80 3.54
Dependent variable is: FY GPA
No Selector
squared squared (adjusted)
with degrees of freedom
Source Sum of Squares df Mean Square F-ratio Regression 1.92283 1 1.92283 42.9 Residual 0.627867 14 0.044848 Variable Coefticient s.e. of Coeft t-ratio prob Constant -1.56410 0.7306 -2.14 0.0504 HS GPA 1.30527 0.1993 6.55 \leq0.0001
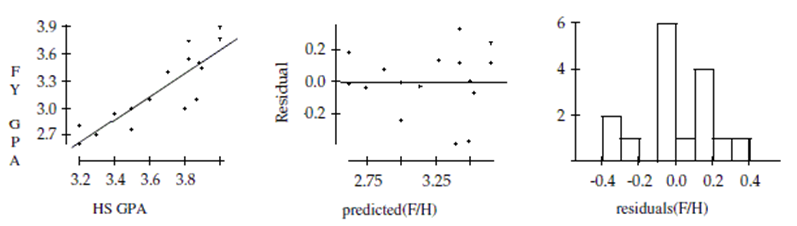 -Is there evidence of an association between high school and first-year college GPAs? Test an appropriate hypothesis and state your conclusion in the proper context.
-Is there evidence of an association between high school and first-year college GPAs? Test an appropriate hypothesis and state your conclusion in the proper context.
(Essay)
4.9/5  (41)
(41)
We want to know whether the categorical variables "eating breakfast" and "student's sex" are statistically independent.
H0: Eating breakfast and student's sex are independent.
HA: There is an association between eating breakfast and student's sex.
Conditions:
*Counted data: We have the counts of individuals in categories of two categorical variables.
*Randomization: We have a convenience sample of students, but no reason to suspect bias.
*Expected cell frequency: The expected values (shown in parenthesis in the table) are all greater than 5, so the condition is satisfied.
Under these conditions, the sampling distribution of the test statistic is ç2 with (r - 1)(c - 1) = (2 - 1)(2 - 1) = 1 degree of freedom, and we will perform a chi-square test of independence.
(Essay)
4.8/5  (32)
(32)
Several volunteers engage in a special exercise program intended to lower their blood pressure. We measure each person's initial blood pressure, lead them through the exercises daily for a month, then check blood pressures again. To see if the program lowered blood pressure significantly we should do a
(Multiple Choice)
4.8/5  (37)
(37)
How many degrees of freedom are there for a chi-square test of independence based on a table with five rows and six columns?
(Multiple Choice)
4.8/5  (39)
(39)
Cloning A random sample of 800 adults was asked the following question: "Do you think
current laws concerning the use of cloning for medical research are too strict, too lenient, or about
right?" The pollsters also classified the respondents with respect to highest education level attained: high school, 2-year college degree, 4-year degree, or advanced degree. We wish to know if attitudes on cloning are related to education level. (All the conditions are satisfied - don't worry about checking them.)
Strict Lenient Right Total High school 93 107 182 382 106.01 87.38 188.61 2-year 27 28.31 19 23.33 56 50.36 102 year 82 75.48 7 62.22 140 134.30 44 Adv. degree 20 7 17 44 12.21 10.07 21.73 Total 222 183 395 800
\chi squared equals 1.60+4.40+0.23+ 0.06+0.80+0.63+ 0.56+2.40+0.24+ 4.97+0.93+1.03=17.86 p=0.0066
a. Write appropriate hypotheses.
b. Suppose the expected counts had not been given. Show how to calculate the expected count in the first cell (106.01).
c. How many degrees of freedom?
d. State your complete conclusion in context.
(Essay)
4.9/5  (42)
(42)
For the scenario described below, simply name the procedure that is appropriate to answer the question. For example,
1-proportion z-interval or chi-square goodness of fit test. Do NOT carry out the procedure.
-In a study on insomnia in men over the age of 65, it is found that exercise may play a role in sleep. The researchers assign a group of 100 men to exercise for a month, while another
100 volunteers are asked to abstain from most exercise. At the end of the month, the exercise group had 23 out of 100 men with difficulty in sleeping, whereas the non-exercise group had 31 out of 100. Does this provide statistically significant that exercise improves sleep for men over 65?
(Essay)
4.8/5  (33)
(33)
Height and weight Is the height of a man related to his weight? The regression analysis from a sample of 26 men is shown. (Show work. Don't write hypotheses. Assume the assumptions for inference were satisfied.) Dependent variable is: Variable Coefficient Weight(lbs) s.e. of coeff Constant -449.61 93.28 Height(inches) 8.737 1.312
a. How many degrees of freedom?
b. What is the value of the t statistic?
c. What is the P-value?
d. State your conclusion in context.
(Essay)
4.7/5  (40)
(40)
Suppose you were asked to analyze each of the situations described below. (NOTE: DO NOT DO THESE PROBLEMS!) For each, indicate which inference procedure you would use (from the list), the test statistic (z, t, or ç? ), and, if t or ç?, the number of degrees of freedom.
Type z, t , or d f a. b. c. d. e. f. g. h.
1. proportion, 1 sample
2. difference of proportions, 2 samples
3. mean, 1 sample
4. mean of differences, matched pairs
5. difference of means, independent samples
6. goodness of fit
7. homogeneity
8. independence
9. regression, inference for )
a. A researcher wonders if meat in the diet may be a factor in high blood pressure. She
compares the blood pressures of 40 randomly selected vegetarians, to those of 40 people who eat meat.
b. According to the American Red Cross, 45% of Americans have Type O blood, 40% Type A, 11% Type B, and 4% Type AB. Last week a blood drive at the high school collected 132 pints of blood. If 51 were Type O, 55 Type A, 17 Type B, and 9 were Type AB, was this yield unusual in any way?
c. Among a random sample of college-age drivers 5% of the 576 men said they had been ticketed for speeding during the past year, compared to only 3% of the 552 women. Does this indicate a significant difference between college males and females in terms of being ticketed for speeding?
d. Who is paid more in New York State - teachers or policemen? We select a random sample of 25 New York cities and find the starting salaries of teachers and policemen in each.
e. Researchers offer small cookies to nine nursery school children and record the number of cookies consumed by each. Forty-five minutes later they observe these children during recess, and rate each child for hyperactivity on a scale from 1 - 20. Is there any evidence that sugar contributes to hyperactivity in children?
f. 22 people complaining of indigestion take an antacid. They report that their discomfort subsided in an average of 13 minutes; the standard deviation was 4 minutes. The manufacturer wants a 95% confidence interval for the "relief time."
g. A sports fan selected a random sample of 100 games from each of the NBA, the NFL, the NHL, and Major League Baseball to see if overtimes (or extra innings) are equally likely to occur in all four sports.
h. A teacher believes that no more than 10% of high school students ever cheat on an exam, but a confidential survey found that 14 of 88 randomly selected students admitted having cheated at least once. Is this strong evidence that the teacher was wrong?
(Essay)
4.9/5  (36)
(36)
The vast majority of states and the District of Columbia have adopted the Common Core State Standards (CCSS) for math and English language arts. Do teachers support the CCSS? In March 2003, The American Federal of Teachers (AFT) asked AFT member teachers "Based on what you know about the Common Core State Standards and the expectations they set for children, do you approve or disapprove of your state's decision to adopt them?
" The following results were reported in American Educator (Volume 32, No. 2, Summer 2013, pg. 3): 27% Strongly Approve; 48% Somewhat Approve; 14% Somewhat Disapprove; 8% Strongly Approve; 3% Not Sure.
A district superintendent asked the same question to the teachers in her district to assess the level of teacher support for the CCSS within the district. She obtained the following results.
Response Strongly Somewhat Somewhat Strongly Not Sure Approve Approve Disapprove Disapprove Frequency 55 106 28 32 9
a. Test an appropriate hypothesis to ascertain if the district CCSS approval distribution matches the national AFT approval distribution.
b. Which response impacted your decision the most? Explain what this means in the context of the problem.
(Essay)
4.9/5  (40)
(40)
Suppose that after the study described in #5 we want to see if there's evidence that the exercise program's effectiveness in lowering blood pressure depends on how high the person's initial blood pressure was. We should do a
(Multiple Choice)
4.9/5  (39)
(39)
Height and weight Last fall, as our first example of correlation, we looked at the heights and weights of some AP* Statistics students. Here are the scatterplot, the residuals plot, a histogram of the residuals, and the regression analysis for the data we collected from the males. Use this information to analyze the association between heights and weights of teenage boys.
Dependent variable is:WT(lb)
squared
Variable Coefficient s.e. of Coeff t-ratio prob Const -364.403 94.61 -3.85 0.0008 HT(in) 7.29993 1.333 5.48 \leq0.0001
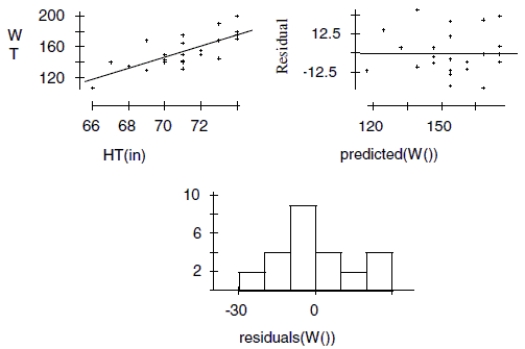 a. Is there an association? Write appropriate hypotheses. b. Are the assumptions for regression satisfied? Explain. c. What do you conclude?
d. Create a 95% confidence interval for the true slope.
e. Explain in context what your interval means.
a. Is there an association? Write appropriate hypotheses. b. Are the assumptions for regression satisfied? Explain. c. What do you conclude?
d. Create a 95% confidence interval for the true slope.
e. Explain in context what your interval means.
(Essay)
4.8/5  (42)
(42)
Suppose you were asked to analyze each of the situations described below. (NOTE: DO NOT DO THESE PROBLEMS!) For each, indicate which inference procedure you would use (from the list), the test statistic (z, t, or ç₂ ), and, if t or ç₂ , the number of degrees of freedom. Type z,t, or df a. b. c. d. e. f. g. h. 1. proportion, 1 sample 2. difference of proportions, 2 samples 3. mean, 1 sample 4. mean of differences, matched pairs 5. difference of means, independent samples 6. goodness of fit 7. homogeneity 8. independence 9. regression, inference for )
a. Doctors offer small candies to sixty teenagers, recording the number of candies consumed by each. One hour later they test the blood sugar level for each person. Is there any evidence that high blood sugar levels in teenagers are related to the amount of candy eaten?
b. Which takes less time to travel to work -- car or train? We select a random sample of 45 businessmen and compare their travel time to work for both types of commute.
c. An orthodontist wonders if soda in the diet may be a factor in loose cement on children's braces. She checks the cement bonds of 40 randomly selected patients who do not drink soda, and 40 patients who do drink soda.
d. Forty people complaining of allergies take an antihistamine. They report that their discomfort subsided in an average of 18 minutes; the standard deviation was 4 minutes. The manufacturer wants a 95% confidence interval for the "relief time".
e. A health professional selected a random sample of 100 patients from each of four major hospital emergency rooms to see if the primary reasons for emergency room visits are similar in all four major hospitals. The primary reasons were categorized as accident, illegal activity, illness, or other.
f. A policeman believes that more than 40% of older drivers speed on highways, but a confidential survey found that 49 of 88 randomly selected older drivers admitted speeding on highways at least once. Is this strong evidence that the policeman was wrong?
g. According to United Nations Population Division, the age distribution of the Commonwealth of Australia is: 21% less than 15 years of age, 67% between 15 and 65 years of age, and 12% are over 65 years old. A random sample of 210 residents of Canberra revealed 40 were less than 15 years of age, 145 were between 15 and 65 years of age, and 25 were over 65 years old. Are the ages of Canberra residents unusual in any way?
h. Among a random sample of college-age students, 6% of the 473 men said they had been adopted, compared to only 4% of the 552 women. Does this indicate a significant difference between adoption rates of males and females in college-age students?
(Essay)
4.9/5  (33)
(33)
Of the 23 first year male students at State U. admitted from Jim Thorpe High School, 8 were offered baseball scholarships and 7 were offered football scholarships. The University admissions committee looked at the students' composite ACT scores (shown in table), wondering if the University was lowering their standards for athletes. Assuming that this group of students is representative of all admitted students, what do you think?
Baseball Non-athletes Football 25 21 22 22 27 21 19 29 24 25 26 27 24 30 19 25 27 23 24 26 17 23 23
Boxplots:
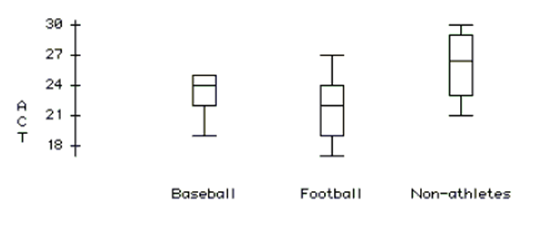 Sums of Mean P- Source Squares df Squares F-ratio value Team 71.00 2 35.50 4.56 0.023 Error 155.61 20 7.78 Total 226.61 22
Level Number Mean Std Dev Baseball 8 23.3750 2.06588 Football 7 21.8571 3.28778 Non Athlete 8 26.1250 2.94897
Normal Probability Plot:
Sums of Mean P- Source Squares df Squares F-ratio value Team 71.00 2 35.50 4.56 0.023 Error 155.61 20 7.78 Total 226.61 22
Level Number Mean Std Dev Baseball 8 23.3750 2.06588 Football 7 21.8571 3.28778 Non Athlete 8 26.1250 2.94897
Normal Probability Plot:
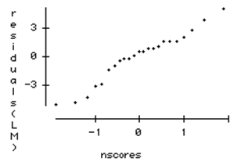 -Test an appropriate hypothesis and state your conclusion
-Test an appropriate hypothesis and state your conclusion
(Essay)
4.9/5  (43)
(43)
In the study "The Role of Sports as a Social Determinant for Children," student respondents in grades 4 through 6 were asked what they would most like to do at school: make good grades, be popular or be good at sports. Results delineated by type of school district are reported below. Rural Suburban Urban Make Good Grades 57 87 24 Be Popular 50 42 6 Be Good at Sports 42 22 5
Source: Chase, M.A and Dummer, G.M. (1992), "The Role of Sports as a Social Determinant for
Children," Research Quarterly for Exercise and Sport, 63, 418-424.
Is there evidence that type of school district and personal school goals are independent? Test an appropriate hypothesis. Give Statistical evidence to support your conclusion.
(Essay)
4.8/5  (35)
(35)
Carnivores A random sample of some of the heaviest carnivores on Earth was reviewed to determine if there is an association between the length (in meters) and weight (in kilograms) of these carnivores. Here are the scatterplot, the residuals plot, a histogram of the residuals, and the regression analysis of the data. Use this information to analyze the association between the length and weight of these carnivores.
The regression equation is
Weight Length
Predictor Coef SE Coef T P Constant -668.3 232.8 -2.87 0.024 Length 485.21 90.63 5.35 0.001
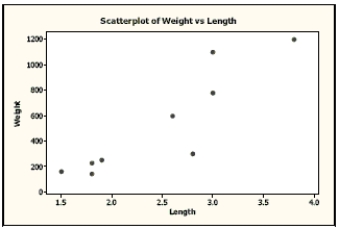
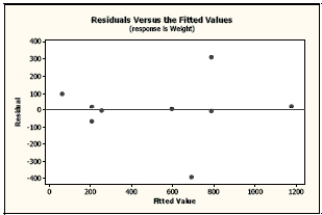
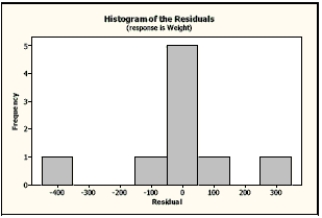 a. Is there an association? Write appropriate hypotheses.
b. Are the assumptions for regression satisfied? Explain.
c. What do you conclude?
d. Create a 98% confidence interval for the true slope.
e. Explain in context what your interval means.
a. Is there an association? Write appropriate hypotheses.
b. Are the assumptions for regression satisfied? Explain.
c. What do you conclude?
d. Create a 98% confidence interval for the true slope.
e. Explain in context what your interval means.
(Essay)
4.9/5  (36)
(36)
Car colors According to Ward's Communication, 19% of sports car enthusiasts prefer a red color, 16.2% silver, 14.7% black, 14.1% green, 14% white, and 22% other colors. A sample of
250 cars at a NASCAR raceway revealed 45 red cars, 42 silver cars, 34 black cars, 40 green cars, 39 white cars, and 50 other color cars. Are NASCAR color preferences typical of sports car enthusiasts? Test an appropriate hypothesis and state your conclusion.
(Essay)
4.8/5  (37)
(37)
Of the 23 first year male students at State U. admitted from Jim Thorpe High School, 8 were offered baseball scholarships and 7 were offered football scholarships. The University admissions committee looked at the students' composite ACT scores (shown in table), wondering if the University was lowering their standards for athletes. Assuming that this group of students is representative of all admitted students, what do you think?
Baseball Non-athletes Football 25 21 22 22 27 21 19 29 24 25 26 27 24 30 19 25 27 23 24 26 17 23 23
Boxplots:
 Sums of Mean P- Source Squares df Squares F-ratio value Team 71.00 2 35.50 4.56 0.023 Error 155.61 20 7.78 Total 226.61 22
Level Number Mean Std Dev Baseball 8 23.3750 2.06588 Football 7 21.8571 3.28778 Non Athlete 8 26.1250 2.94897
Normal Probability Plot:
Sums of Mean P- Source Squares df Squares F-ratio value Team 71.00 2 35.50 4.56 0.023 Error 155.61 20 7.78 Total 226.61 22
Level Number Mean Std Dev Baseball 8 23.3750 2.06588 Football 7 21.8571 3.28778 Non Athlete 8 26.1250 2.94897
Normal Probability Plot:
 -Are the two sports teams mean ACT scores different?
-Are the two sports teams mean ACT scores different?
(Essay)
4.8/5  (43)
(43)
When two competing teams are equally matched, the probability that each team wins any game is 0.5. The NBA championship goes to the team that wins four games in a
best-of-seven series. If the teams were equally matched, the probability that the final series ends with one of the teams sweeping four straight games would be 2(0.5)4 = 0.125. Further probability calculations indicate that 25% of these series should last five games, 31.25% should last six games, and the other 31.25% should last the full seven games. The table shows the number of games it took to decide each of the last 57 NBA champs. Do you think the teams are usually equally matched? Give statistical evidence to support yourconclusion.
Length of series 4 games 5 games 6 games 7 games NBA finals 7 13 22 15
(Essay)
4.8/5  (37)
(37)
Peanut M&Ms According to the Mars Candy Company, peanut M&M's are 12% brown,
15% yellow, 12% red, 23% blue, 23% orange, and 15% green. On a Saturday when you have
run out of statistics homework, you decide to test this claim. You purchase a medium bag
of peanut M&M's and find 39 browns, 44 yellows, 36 red, 78 blue, 73 orange, and 48 greens. Test an appropriate hypothesis and state your conclusion.
(Essay)
4.8/5  (45)
(45)
Showing 21 - 40 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)