Exam 10: Propositional Logic-Arguments
Exam 1: Classification93 Questions
Exam 2: Definitions105 Questions
Exam 3: Propositions145 Questions
Exam 4: Argument Analysis144 Questions
Exam 5: Fallacies167 Questions
Exam 6: Categorical Propositions218 Questions
Exam 7: Categorical Syllogisms223 Questions
Exam 8: Reasoning With Syllogisms177 Questions
Exam 9: Propositional Logic-Propositions223 Questions
Exam 10: Propositional Logic-Arguments120 Questions
Exam 11: Predicate Logic147 Questions
Exam 12: Inductive Generalizations56 Questions
Exam 13: Argument by Analogy47 Questions
Exam 14: Statistical Reasoning82 Questions
Exam 15: Explanation55 Questions
Exam 16: Probability85 Questions
Select questions type
The following argument is an instance of one of the five inference forms Simp, Conj, Add, CD, DD.Identify the form.
(Multiple Choice)
4.9/5  (33)
(33)
Which rule is used in the following inference? [(A\cdotB)\cup(C\supsetD)]v(E\supsetF) (A\cdotB)v(C\supsetD)
(Multiple Choice)
4.9/5  (40)
(40)
The following argument is an instance of one of the five inference forms Simp, Conj, Add, CD, DD.Identify the form. R
(Multiple Choice)
4.8/5  (36)
(36)
Which rule is used in the following inference? A\supset(D\veeF) (D\veeF)\supsetG A\supsetG
(Multiple Choice)
4.8/5  (34)
(34)
Which rule is used in the following inference? F\supsetG \simA\vee(F\supsetG)
(Multiple Choice)
4.8/5  (37)
(37)
The following argument is an instance of one of the five inference forms MP, MT, HS, DS, Conj.Identify the form. 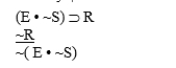
(Multiple Choice)
4.8/5  (28)
(28)
Use a short form truth table to answer the following question.Which, if any, set of truth values assigned to the atomic sentences shows that the following argument is invalid? (\cdot)\supset (\cdot)\supset(\cdot) (\cdot)\supset
(Multiple Choice)
4.7/5  (25)
(25)
Use a truth table to answer the following question.Which, if any, set of truth values assigned to the atomic sentences shows that the following argument is invalid?
(Multiple Choice)
4.9/5  (31)
(31)
Which rule is used in the following inference? (\supset)\cdot(\sim\vee) [(\supset)\cdot(\sim\vee)]\cdot[(\equiv\sim)\vee(\cdot\sim)]
(Multiple Choice)
4.7/5  (31)
(31)
Use a short form truth table to answer the following question.Which, if any, set of truth values assigned to the atomic sentences shows that the following argument is invalid? (\bullet\sim)\supset(\vee) \sim \sim \sim
(Multiple Choice)
4.9/5  (37)
(37)
Which rule is used in the following inference? (\vee)\cup(\cdot) ?
(Multiple Choice)
4.7/5  (34)
(34)
Which rule is used in the following inference? [(A\supsetB)\vee(C\supsetB)]\supset\sim(\simA\cdot\simC) (A\supsetB)\vee(C\supsetB) \sim(\simA\cdot\simC)
(Multiple Choice)
4.7/5  (40)
(40)
The following argument is an instance of one of the five inference forms Simp, Conj, Add, CD, DD.Identify the form.
(Multiple Choice)
4.8/5  (34)
(34)
Use a truth table to answer the following question.Which, if any, set of truth values assigned to the atomic sentences shows that the following argument is invalid?
(Multiple Choice)
4.7/5  (34)
(34)
The following argument is an instance of one of the five inference forms MP, MT, HS, DS, Conj.Identify the form. (\supset)\supset(\vee) (\vee)\supset(\equivW) (\supset)\supset(\equivW)
(Multiple Choice)
4.7/5  (29)
(29)
The following argument is an instance of one of the five inference forms MP, MT, HS, DS, Conj.Identify the form. (U\cupW)\supsetS S\supsetC (U\veeW)\supsetC
(Multiple Choice)
4.8/5  (38)
(38)
Which, if any, of the following proofs are correct demonstrations of the validity of this argument? Proof 1 (1)(P\cdotQ)\cdot(R\veeS) /Q Premise/Conclusion (2) P\cdotQ 1 (3) R\veeS 1 (4) P 2 (5) Q 2 Proof 2 (1) (\cdot)\cdot(\vee) / Premise/Conclusion (2) P\cdotQ 1 (3) Q 2
(Multiple Choice)
4.7/5  (38)
(38)
Use a truth table to answer the following question.Which, if any, set of truth values assigned to the atomic sentences shows that the following argument is invalid? A\cupB
(Multiple Choice)
4.7/5  (34)
(34)
Which rule is used in the following inference? (B\cdotC)\veeD \sim B\cdotC
(Multiple Choice)
4.8/5  (35)
(35)
The following argument is an instance of one of the five inference forms MP, MT, HS, DS, Conj.Identify the form. \equiv (\equiv)\supset(\cdot) \cdot
(Multiple Choice)
4.9/5  (27)
(27)
Showing 41 - 60 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)