Exam 14: Introduction to Multiple Regression

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixthgrade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. 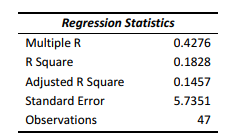Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = Salaries and X ₂ = Spending: 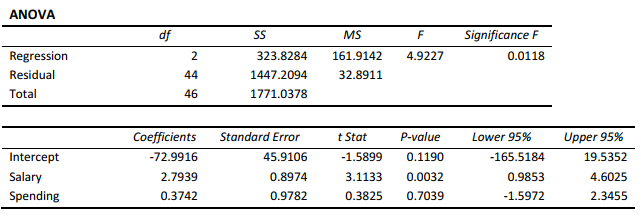-Referring to Scenario 14-15,there is sufficient evidence that at least one of the explanatory variables is related to the percentage of students passing the proficiency test at a 5% level of significance.

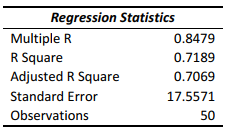
SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: 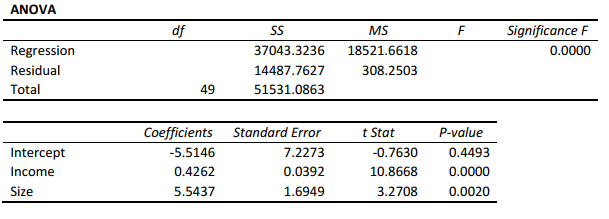Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-4,the value of the partial F test statistic is _____for H₀ : Variable X₁ does not significantly improve the model after variable X₂ has been included H₁ : Variable X₁ significantly improves the model after variable X₂ has been included

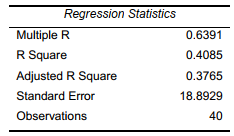
SCENARIO 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age)and a dummy variable for management position (Manager: 1 = yes,0 = no). The results of the regression analysis are given below: 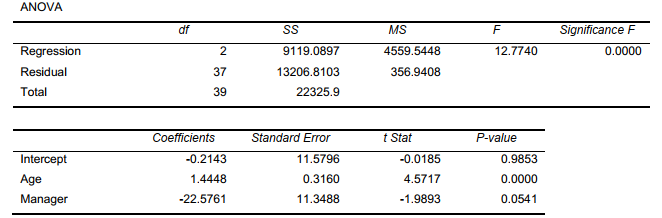-Referring to Scenario 14-17,which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of the other independent variable?

SCENARIO 14-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X₁ ) and the amount of insulation in inches ( X ₂ ). Given below is EXCEL output of the regression model. 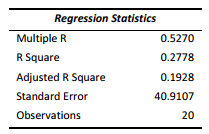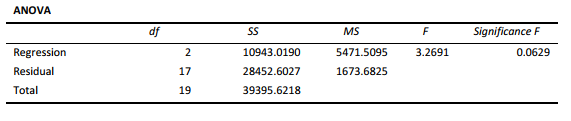Also SSR (X₁ | X₂) = 8343.3572 and SSR (X₂ | X₁) = 4199.2672 -Referring to Scenario 14-5,what is the p-value for Capital?

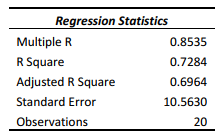
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X₁ = Age) and experience in the field (X₂ = Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: 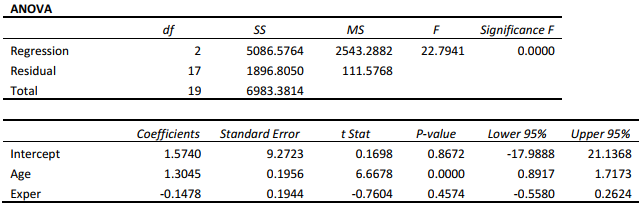Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8,the analyst wants to use a t test to test for the significance of the coefficient of X₂.The value of the test statistic is .

SCENARIO 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age)and a dummy variable for management position (Manager: 1 = yes,0 = no). The results of the regression analysis are given below: -Referring to Scenario 14-17,the null hypothesis should be rejected at a 10% level of significance when testing whether there is a significant relationship between the number of weeks a worker is unemployed due to a layoff and the entire set of explanatory variables.

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixthgrade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = Salaries and X ₂ = Spending: -Referring to Scenario 14-15,what is the value of the test statistic when testing whether mean teacher salary has any effect on percentage of students passing the proficiency test,considering the effect of instructional spending per pupil?

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-3,to test for the significance of the coefficient on aggregate price index,the p-value is

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-4,which of the following values for the level of significance is the smallest for which at most one explanatory variable is significant individually?

SCENARIO 14-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X₁ ) and the amount of insulation in inches ( X ₂ ). Given below is EXCEL output of the regression model. Also SSR (X₁ | X₂) = 8343.3572 and SSR (X₂ | X₁) = 4199.2672 -Referring to Scenario 14-6,the partial F test for H₀ : Variable X₁ does not significantly improve the model after variable X₂ has been included H₁ : Variable X₁ significantly improves the model after variable X₂ has been included has _____ and _____ degrees of freedom.

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixthgrade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = Salaries and X ₂ = Spending: -Referring to Scenario 14-15,you can conclude that instructional spending per pupil has no impact on the mean percentage of students passing the proficiency test,considering the effect of mean teacher salary,at a 5% level of significance using the confidence interval estimate for $\beta$ ₂.

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X₁ = Age) and experience in the field (X₂ = Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-7,the predicted GPA for a student carrying 15 course units and who has a total SAT of 1,100 is .

SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixthgrade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = Salaries and X ₂ = Spending: -Referring to Scenario 14-15,there is sufficient evidence that both of the explanatory variables are related to the percentage of students passing the proficiency test at a 5% level of significance.

SCENARIO 14-18 A logistic regression model was estimated in order to predict the probability that a randomly chosen university or college would be a private university using information on mean total Scholastic Aptitude Test score (SAT) at the university or college and whether the TOEFL criterion is at least 90 (Toefl90 = 1 if yes, 0 otherwise.) The dependent variable, Y, is school type (Type = 1 if private and 0 otherwise). There are 80 universities in the sample. The PHStat output is given below: 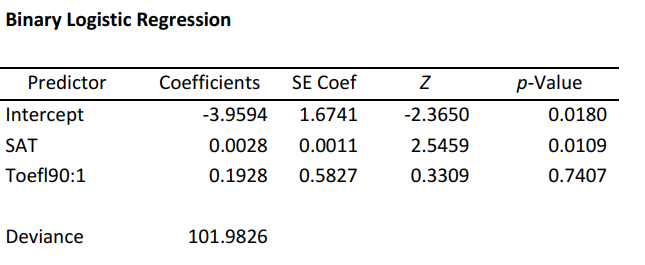-Referring to Scenario 14-18, what is the estimated probability that a school with a mean SAT score of 1100 and a TOEFL criterion that is not at least 90?

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-4 and allowing for a 1% probability of committing a type I error,what is ^{the decision and conclusion for the test} H₀ : $\beta$ ₁ = $\beta$ ₂ $\neq$ 0 vs.H₁ : At least one $\beta$ _j $\neq$ 0,j = 1,2 ?

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X₁ = Age) and experience in the field (X₂ = Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8,the analyst decided to construct a 95% confidence interval for $\beta$ ₂ .The confidence interval is from _____ to _____ .

SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X₁ = Age) and experience in the field (X₂ = Exper). He took a sample of 20 employees and obtained the following Microsoft Excel output: Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848. -Referring to Scenario 14-8,the estimate of the unit change in the mean of Y per unit change in X₁,considering the effects of the other variable,is .

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-4,what annual income (in thousands of dollars)would an individual with a family size of 4 need to attain a predicted 10,000 square foot home (House = 100)?

SCENARIO 14-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size). House size is measured in hundreds of square feet and income is measured in thousands of dollars. The builder randomly selected 50 families and ran the multiple regression. Partial Microsoft Excel output is provided below: Also SSR (X₁ | X₂) = 36400.6326 and SSR (X₁ | X₂) = 3297.7917 -Referring to Scenario 14-3,the p-value for GDP is

SCENARIO 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age)and a dummy variable for management position (Manager: 1 = yes,0 = no). The results of the regression analysis are given below: -Referring to Scenario 14-17,the null hypothesis H₀: $\beta$ ₁= $\beta$ ₂=0implies that the number of weeks a worker is unemployed due to a layoff is not related to any of the explanatory variables.