Exam 8: Calculus of Several Variables
Exam 1: Preliminaries209 Questions
Exam 2: Functions, Limits and the Derivative271 Questions
Exam 3: Differentiation331 Questions
Exam 4: Applications of the Derivative183 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration313 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables205 Questions
Select questions type
Find the critical point(s) of the function.Then use the second derivative test to classify the nature of each point, if possible.Finally, determine the relative extrema of the function. 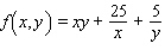 Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
(Essay)
4.9/5  (33)
(33)
The IQ (itelligence quotient) of a person whose mental age is 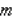 years and whose chronological age is
years and whose chronological age is  years is defined as
years is defined as 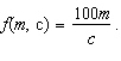 What is the IQ of a 10-years-old child who has a mental age of 19 years?
What is the IQ of a 10-years-old child who has a mental age of 19 years?
(Multiple Choice)
4.8/5  (43)
(43)
Find the critical point(s) of the function.Then use the second derivative test to classify the nature of each point, if possible.Finally, determine the relative extrema of the function. 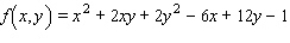 Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
Find the critical point(s) of the function.
Find the point(s) of maximum.
Find the point(s) of minimum.
Find the relative extrema of the function.
(Essay)
4.7/5  (29)
(29)
An open rectangular box is to be constructed from material that costs 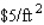 for the bottom and
for the bottom and 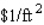 for its sides.Find the dimensions of the box of greatest volume that can be constructed for
for its sides.Find the dimensions of the box of greatest volume that can be constructed for 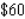 .
.
(Multiple Choice)
4.7/5  (35)
(35)
Determine whether the statement is true or false.If it is true, explain why it is true.If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then ![Determine whether the statement is true or false.If it is true, explain why it is true.If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB7866/11eb12b0_a920_1c8c_b394_e70dee95e5ef_TB7866_11.jpg) where
where ![Determine whether the statement is true or false.If it is true, explain why it is true.If it is false, give an example to show why it is false. If h(x, y) = f(x)g(y), where f is continuous on [a, b] and g is continuous on [c, d], then where](https://storage.examlex.com/TB7866/11eb12b0_a920_1c8d_b394_4f2effb19f83_TB7866_11.jpg)
(Multiple Choice)
4.8/5  (29)
(29)
Evaluate the double integral 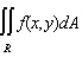 for the function
for the function 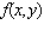 and the region R.
and the region R. 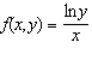 and R is the rectangle defined by
and R is the rectangle defined by 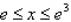 and
and 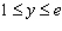 .
.
(Short Answer)
4.8/5  (40)
(40)
Because of new, lower standards, experts in a study conducted in early 2000 projected a rise in the market for cholesterol-reducing drugs.The any market (in billions of dollars) for such drugs from 1999 through 2004 is given in the following table ( 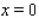 represents 1999):
represents 1999):  Find an equation of the least-squares line for these data.Please round coefficients to the nearest hundredth if necessary.Estimate the market for cholesterol-reducing drugs in 2005, assuming the trend continued.
Find an equation of the least-squares line for these data.Please round coefficients to the nearest hundredth if necessary.Estimate the market for cholesterol-reducing drugs in 2005, assuming the trend continued.
(Multiple Choice)
4.9/5  (28)
(28)
Find the equation of the least-squares line for the given data.Draw a scatter diagram for the given data and graph the least-squares line.  Please round the coefficients in your equation to two decimal places.
Please round the coefficients in your equation to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Find the critical point(s) of the function.Then use the second derivative test to classify the nature of each point, if possible.Finally, determine the relative extrema of the function. 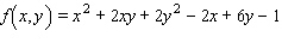
(Multiple Choice)
4.7/5  (43)
(43)
Use a double integral to find the volume of the solid shown in the figure. 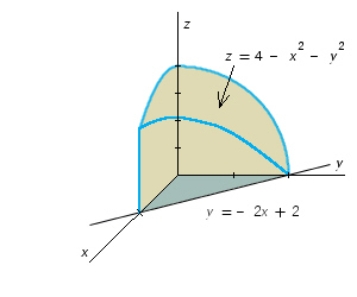
(Multiple Choice)
4.8/5  (32)
(32)
Postal regulations specify that the combined length and girth of a parcel sent by parcel post may not exceed 132 in.Find the dimensions of the rectangular package that would have the greatest possible volume under these regulations.(Hint: Let the dimensions of the box be 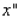 by
by 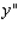 by
by 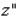 (see the figure below).Then,
(see the figure below).Then, 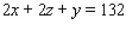 , and the volume
, and the volume 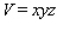 .So that
.So that 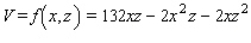 .Maximize
.Maximize 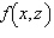 .)
.) 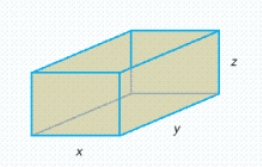 x = __________ inches
y = __________ inches
z = __________ inches
V = __________ cubic inches
x = __________ inches
y = __________ inches
z = __________ inches
V = __________ cubic inches
(Essay)
4.9/5  (33)
(33)
Evaluate the double integral 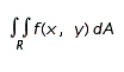 for the function
for the function 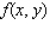 and the region
and the region 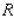 .
.  and
and 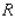 is bounded by
is bounded by 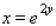 ,
, 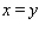 ,
, 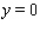 and
and 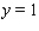 .
.
(Multiple Choice)
4.9/5  (29)
(29)
Evaluate the first partial derivatives of the function at the given point. 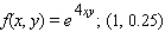
(Multiple Choice)
4.7/5  (32)
(32)
A closed rectangular box having a volume of 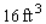 is to be constructed.If the material for the sides costs
is to be constructed.If the material for the sides costs 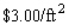 and the material for the top and bottom costs
and the material for the top and bottom costs 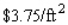 , find the dimensions of the box that can be constructed with minimum cost.
, find the dimensions of the box that can be constructed with minimum cost.
(Essay)
4.8/5  (21)
(21)
Evaluate the double integral 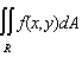 for the given function f(x, y) and the region R. f(x, y) = 5
for the given function f(x, y) and the region R. f(x, y) = 5 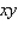 ; R is bounded by the lines x = 1, y = 0 and y = x.
; R is bounded by the lines x = 1, y = 0 and y = x.
(Multiple Choice)
4.9/5  (33)
(33)
In a survey it was determined that the demand equation for VCRs is given by 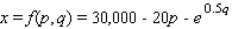 The demand equation for blank VCR tapes is given by
The demand equation for blank VCR tapes is given by 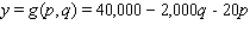 where
where 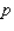 and
and 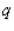 denote the unit prices, respectively, and
denote the unit prices, respectively, and 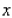 and
and 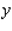 denote the number of VCRs and the number of blank VCR tapes demanded each week.Determine whether these two products are substitute, complementary, or neither.
denote the number of VCRs and the number of blank VCR tapes demanded each week.Determine whether these two products are substitute, complementary, or neither.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 121 - 140 of 205
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)