Exam 11: Correlation and Regression

In an experiment to determine whether there is a systematic difference between the weights obtained with two different mass balances, six specimens were weighed, in grams, on each balance. The following data were obtained: Specimen 1 13.05 13.07 2 6.38 6.40 3 5.00 4.95 4 13.33 13.29 5 10.56 10.55 6 12.92 12.92 State the null and alternate hypotheses.

The following display from a TI-84 Plus calculator presents the results of a hypothesis test for the difference between two proportions. The sample sizes are $n _ { 1 } = 80$ and $n _ { 2 } = 107$ Can you reject $H _ { 0 }$ rejected at the $\alpha = 0.01$ level?

The following display from a TI-84 Plus calculator presents the results of a hypothesis test for the difference between two proportions. The sample sizes are $n _ { 1 } = 95$ and $n _ { 2 } = 104$ What is the P -value?

The football coach at State University wishes to determine if there is a decrease in offensive production between the first half and the second half of his team's recent games. The table below shows the first-half and second-half offensive production (measured in total yards gained per half) for the past six games. 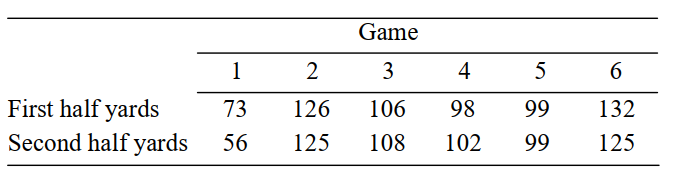Can you conclude that the mean offensive production in the first half differed from that of the second half? i). State the null and alternative hypotheses. ii). Compute the test statistic. iii). State a conclusion using the α = 0.10 level of significance.

The following MINITAB output display presents the results of a hypothesis test on the difference between two proportions. Test and CI for Two Proportions: P1, P2 Variable Sample P P1 43 107 0.40186916 P2 36 95 0.37894737 Difference $= \mathrm { p } ( \mathrm { P } 1 ) = \mathrm { p } ( \mathrm { P } 2 )$ Estimate for differencę.02292179 $95 \%$ CI for difference:(-0.11191015, 0.15775373) T-Test of difference $= 0 ($ vs not $= \mathbb { Z } ) = 0.33320523 \quad$ P-Value $= 0.7389795$ Can you reject $H _ { 0 }$ rejected at the $\alpha = 0.05$ level?

A study reported that in a sample of 104 people who watch television news, 35 had elevated diastolic blood pressure levels (in millimeters of mercury, or mmHg). In a sample of 74 people who do not watch television news, 20 had elevated diastolic blood pressure levels. Can you conclude that the proportion of people with elevated diastolic blood pressure levels differs between news-watchers and those who do not watch news? Use the $\alpha = 0.05$ level significance.

The concentration of hexane (a common solvent) was measured in units of micrograms per liter for a simple random sample of nineteen specimens of untreated ground water taken near a municipal landfill. The sample mean was 508.4 with a sample standard deviation of 4.3. Sixteen specimens of treated ground water had an average hexane concentration of 506.1 with a standard deviation of 4.7. It is reasonable to assume that both samples come from populations that are approximately normal. Can you conclude that the mean hexane concentration is less in treated water than in untreated water? Use the $\alpha = 0.01$ level of significance.

The following MINITAB output display presents the results of a hypothesis test on the difference between two proportions. Test and CI for Two Proportions: P1, P2 Variable Sample P P1 47 88 0.534091 P2 44 89 0.494382 Difference $= \mathrm { p } ( \mathrm { P } 1 ) = \mathrm { p } ( \mathrm { P } 2 )$ Estimate for difference9.039709 $95 \%$ CI for difference:(-0.107557, 0.186975) T-Test of difference $= 0 ($ vs not $= \not ) = 0.528496$ P-Value $= 0.597155$ What is the P-value?

Following is a sample of five matched pairs. Sample 1 18 26 20 20 20 Sample 2 17 20 18 19 18 Let $\mu _ { 1 }$ and $\mu _ { 2 }$ represent the population means and let $\mu _ { \mathrm { d } } = \mu _ { 1 } - \mu _ { 2 }$ . A test will be made of the hypotheses $H _ { 0 } : \mu _ { \mathrm { d } } = 0$ versus $H _ { 1 } : \mu _ { \mathrm { d } } > 0$ . Can you reject $H _ { 0 }$ at the $\alpha = 0.05$ level of significance?

An F-test with 13 degrees of freedom in the numerator and 9 degrees of freedom in the denominator produced a test statistic whose value was 3.36. The null and alternate hypotheses were $H _ { 0 } : \sigma _ { 1 } = \sigma _ { 2 } \text { versus } H _ { 1 } : \sigma _ { 1 } < \sigma _ { 2 } .$ Do you reject $H _ { 0 }$ at the $\alpha = 0.05$ level?

The following MINITAB output display presents the results of a hypothesis test for the difference $\mu _ { 1 } - \mu _ { 2 }$ between two population means. Two-sample T for X1 vs X2 N Mean StDev SE Mean A 7 145.411 24.669 9.324 B 14 132.964 25.604 6.843 Difference $= m u ( X 1 ) - m u ( X 2 )$ Estimate for difference: $12.447$ $95 \%$ CI for difference: $( - 10.222,35.116 )$ $\mathrm { T } -$ Test of difference $= 0 ($ vs not $= ) : \quad$ T-Value $= 1.076209$ $\mathrm { P } -$ Value $= 0.301402 \quad \mathrm { DF } = 13$ What is the alternate hypothesis?

Find the critical value $f _ { 0.10 } \text { for } F _ { 4,11 }$

In an experiment to determine whether there is a systematic difference between the weights obtained with two different mass balances, six specimens were weighed, in grams, on each balance. The following data were obtained: Specimen 1 7.97 7.95 2 10.27 10.25 3 6.70 6.70 4 10.22 10.21 5 7.89 7.88 6 5.10 5.07 State a conclusion using the $\alpha = 0.05$ level of significance.

A broth used to manufacture a pharmaceutical product has its sugar content, in milligrams per milliliter, measured several times on two successive days.The results are shown below. Can you conclude that the variability of the process is greater on the second day than on tl day? Use the $\alpha = 0.10$ level of significance.

The following display from a TI-84 Plus calculator presents the results of a hypothesistest for the difference between two means. The sample sizes are $n _ { 1 } = 10 \text { and } n _ { 2 } = 15$ How many degrees of freedom did the calculator use?

The following display from a TI-84 Plus calculator presents the results of a hypothesis test for the difference between two proportions. The sample sizes are $n _ { 1 } = 108$ and $n _ { 2 } = 75$ Is this a left-tailed test, a right-tailed test, or a two-tailed test?

A test was made of $H _ { 0 } : \mu _ { 1 } = \mu _ { 2 } \text { versus } H _ { 1 } : \mu _ { 1 } < \mu _ { 2 } .$ The sample means were $\bar { x } _ { 1 } = 7$ and $\bar { x } _ { 2 } = 15$ the sample standard deviations were $s _ { 1 } = 3 \text { and } s _ { 2 } = 6$ and the sample sizes were $n _ { 1 } = 19 \text { and } n _ { 2 } = 10$ Is $H _ { 0 }$ rejected at the 0.05 level? (Hint: First compute the value of the test statistic.)

Five null hypotheses were tested, and the P-values were: Hypothesis 1 2 3 4 5 P-value 0.022 0.003 0.018 0.015 0.012 Which hypotheses, if any, can be rejected at the $\alpha = 0.05$ level?

The football coach at State University wishes to determine if there is a change in offensive production between the first half and the second half of his team's recent games. The table below shows the first-half and second-half offensive production (measured in total yards gained per half) for the past six games. Game 1 2 3 4 5 6 First half yards 123 136 130 134 95 93 Second half yards 103 120 116 143 62 60 State the null and alternative hypotheses.

The following display from a TI-84 Plus calculator presents the results of a hypothesis test for the difference between two means. The sample sizes are $n _ { 1 } = 10 \text { and } n _ { 2 } = 7$ What is the P -value?