Exam 5: Systems of Equations and Inequalities
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the number of solutions to the system, and determine whether the system is inconsistent, or the equations are dependent.
- 2x+4y+3z=45 x-y+5z=30 -x+4y+3z=
(Multiple Choice)
4.7/5  (24)
(24)
Graph the solution set. If there is no solution, indicate that the solution set is the empty set.
- +>16 +\leq64
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Camille and Sasha each make an ice cream sundae. Camille gets 2 scoops of Cherry ice cream and 1 scoop of Mint Chocolate Chunk ice cream for a total of 46 g of fat. Sasha has 3 scoops of Cherry ice
Cream and 2 scoop of Mint Chocolate Chunk ice cream for a total of 77 g of fat. How many grams
Of fat does 1 scoop of each type of ice cream have?
(Multiple Choice)
4.8/5  (38)
(38)
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the number of solutions to the system, and determine whether the system is inconsistent, or the equations are dependent.
- b+5c =7 12a-c =18 -6a+3b =-19
(Multiple Choice)
4.7/5  (38)
(38)
Determine if the ordered triple is a solution to the system of equations.
- -4x+8y+2z=-40 -9x+8y+8z=-27;(-4,-6,-1) -8x+6y-8z=14
(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-A basketball player scored 33 points in one game. In basketball, some baskets are worth 3 points, some are worth 2 points, and free-throws are worth 1 point. He scored four more 2-point baskets
Than he did 3-point baskets. The number of free throws equaled the sum of the number of 2-point
And 3-point shots made. How many free-throws did he make?
(Multiple Choice)
4.7/5  (33)
(33)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The points of intersection of a feasible region are called the ________of the region.
(Short Answer)
4.8/5  (41)
(41)
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
-
(Multiple Choice)
4.9/5  (40)
(40)
Use the substitution to rewrite the equations in the system in terms of the variables u and
v. Solve the system in terms of u and v. Then back substitute to determine the solution set to the original
system in terms of x and y.
- +=-4 -=20
(Multiple Choice)
4.8/5  (41)
(41)
Solve the system by the substitution method.
- x-6y=-52 +12y=112
(Multiple Choice)
4.9/5  (30)
(30)
Find the partial fraction decomposition. (Hint: Use the rational zero theorem to factor the denominator.)
-
(Multiple Choice)
4.9/5  (43)
(43)
Choose the one alternative that best completes the statement or answers the question.
Set up the form for the partial fraction decomposition. Do not solve for A, B, C, and so on.
-
(Multiple Choice)
4.8/5  (39)
(39)
Determine the values of x and y that produce the maximum value of the objective function on the feasible
region. Determine the maximum value of the objective function on the feasible region.
- x\geq0,y\geq0 110x+70y\leq8,600 x+y\leq100 Maximize: z=35x+30y
(Multiple Choice)
4.8/5  (37)
(37)
Determine the values of x and y that produce the maximum value of the objective function on the given feasible region.
-
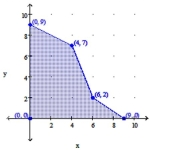
(Multiple Choice)
4.9/5  (45)
(45)
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
- +=3 +=2
(Multiple Choice)
4.7/5  (32)
(32)
Solve the system. If there is more than one solution, write the general solution.
- x+y-2z=9 3x+y+2z=15 x-5y+22z=-27
Solution is any real number
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)