Exam 7: Systems of Equations and Matrices
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
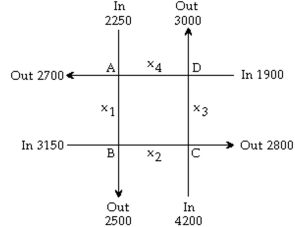
In an analysis of traffic, a certain city estimates the traffic flow as illustrated in the figure below, where the arrows indicate the flow of traffic. If x1 represents the number of cars traveling from intersection A to intersection B, x2 represents the number of cars traveling from intersection B to intersection C , and so on, we car formulate equations based on the principle that the number of vehicles entering the intersection equals the numt leaving it. Formulate an equation for the traffic at each of the four intersections.
(Multiple Choice)
5.0/5  (30)
(30)
The sum of a student's three scores is 230. If the first is 19 points more than the second, and the sum of the first two is 23 more than twice the third, then what was the first score?
(Multiple Choice)
4.9/5  (35)
(35)
Decide whether or not matrix A and matrix B are inverses.
-
(Multiple Choice)
4.8/5  (38)
(38)
A bakery sells three types of cakes. The table below gives the number of cups of flour, cups of sugar, and eggs needed to produce each type of cake. 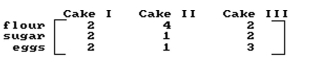 To fill its orders for cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 51 eggs. How many cakes of each
Type were made?
To fill its orders for cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 51 eggs. How many cakes of each
Type were made?
(Multiple Choice)
4.8/5  (37)
(37)
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The total income from the 5% and 6% investments is equal to the income
From the 8% investment. Find the amount invested at each rate.
(Multiple Choice)
4.8/5  (37)
(37)
A $100,000 trust is to be invested in bonds paying 9%, CDs paying 7%, and mortgages paying 10%. The sum of the bond and CD investment must equal the mortgage investment. To earn an $9100 annual income from the
Investments, how much should the bank invest in bonds?
(Multiple Choice)
4.9/5  (33)
(33)
Use an inverse matrix to find the solution to the system.
-Suppose that in a certain city, the Democratic, Republican, and Independent parties always nominate candidates mayor. It turns out that the percent of people voting for each party candidate in the next election depends on the that voted for that party in the last election. The percent voting for each party in the next election is given by
where , and are the respective percents (in decimals) that voted for that party in the last election. If the perce voting for a Democrat in the next election is , the percent voting for a Republican in the next election is , and the percent voting for the Independent party in the next election is , then what percent of people voted for an Independent in the last election?
(Multiple Choice)
4.9/5  (32)
(32)
Solve using Cramer's rule, if possible. If it is not possible, state whether the system is inconsistent or has infinitely many
solutions.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the system graphically.
-The sum of the areas of two square plots of land is and the difference of their areas is . Find a length of a side of each plot.
(Multiple Choice)
4.7/5  (44)
(44)
Showing 161 - 180 of 196
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)