Exam 7: Systems of Equations and Matrices
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
Solve using Cramer's Rule.
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a 109-pound force is applied at the peak of the truss, then the forces or weights and exerted parallel to each rafter of the truss are determined by the following linear system of equations. Solve the system to find and .
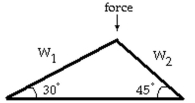
(Multiple Choice)
4.8/5  (36)
(36)
Solve using Cramer's Rule.
-Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a force of 124 pounds is applied at the peak of the truss, then the forces or weights and exerted parallel to each rafter of the truss are determined by the following linear system of equations. Solve the system to find and .
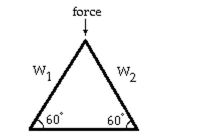 + =124 -=0
+ =124 -=0
(Multiple Choice)
4.8/5  (37)
(37)
Find the solution or solutions, if any exist, to the system.
-
(Multiple Choice)
4.9/5  (32)
(32)
Decide whether or not matrix A and matrix B are inverses.
-
(Multiple Choice)
4.8/5  (24)
(24)
A basketball fieldhouse seats 15,000. Courtside seats sell for $8, endzone for $7, and balcony for $5. A full house earns $88,000 in ticket revenue. If half the courtside and balcony seats and all the endzone seats are sold, the
Total ticket revenue is $51,000. How many of each type of seat are there?
(Multiple Choice)
4.7/5  (41)
(41)
A company produces three types of bookcases: 4-shelf metal, 6-shelf metal, and 4-shelf wooden. The 4-shelf metal bookcase requires 2.5 hours for fabrication, one hour to paint, and one-half hour to package for shipping.
The 6-shelf bookcase requires 4 hours for fabrication, 1.5 hours to paint, and one-half hour to package. The
Wooden bookcase requires 3 hours to fabricate, 2 hours to paint, and one-half hour to package. The daily
Number of hours available for each phase of production are: 167 for fabrication, 81 for painting, and 26 for
Packaging. How many of each type of bookcase can the company produce in one day?
(Multiple Choice)
4.9/5  (41)
(41)
first two games of the season. Write a matrix containing the total number of points and rebounds for each of the starting
five.
Game 1 Points Rebounds Levy 20 3 Cowens 16 5 Williams 8 12 Miller 6 11 Jenkins 10 2 Game 2 Points Rebounds Levy 18 4 Cowens 14 3 Williams 12 9 Miller 4 10 Jenkins 10 3
A)
В)
C)
D) Answer: C
-A bakery sells four main items: rolls, bread, cake, and pie. The amount of each of five ingredients (in cups, except for eggs) required to make a dozen rolls, a loaf of bread, a cake, or a pie is given by matrix A. ![first two games of the season. Write a matrix containing the total number of points and rebounds for each of the starting five. \begin{array}{l} \begin{array} { l | c | c } \text { Game } 1 & \text { Points } & \text { Rebounds } \\ \hline \text { Levy } & 20 & 3 \\ \text { Cowens } & 16 & 5 \\ \text { Williams } & 8 & 12 \\ \text { Miller } & 6 & 11 \\ \text { Jenkins } & 10 & 2 \end{array}\\\\ \begin{array} { l | c | c } \text { Game } 2 & \text { Points } & \text { Rebounds } \\ \hline \text { Levy } & 18 & 4 \\ \text { Cowens } & 14 & 3 \\ \text { Williams } & 12 & 9 \\ \text { Miller } & 4 & 10 \\ \text { Jenkins } & 10 & 3 \end{array} \end{array} A) \left[ \begin{array} { l l } 5 & 62 \end{array} \right] В) \left[ \begin{array} { r r } 7 & 38 \\ 30 & 8 \\ 21 & 20 \\ 21 & 10 \\ 5 & 20 \end{array} \right] C) \left[ \begin{array} { r r } 38 & 7 \\ 30 & 8 \\ 20 & 21 \\ 10 & 21 \\ 20 & 5 \end{array} \right] D) [ 625 ] Answer: C -A bakery sells four main items: rolls, bread, cake, and pie. The amount of each of five ingredients (in cups, except for eggs) required to make a dozen rolls, a loaf of bread, a cake, or a pie is given by matrix A. The cost (in cents) per unit of ingredient when purchased in large lots or small lots is given in matrix B. Use m Cost Large Lot Small Lot \left[ \begin{array} { l } \text { Eggs } \\ \text { Flour } \\ \text { Sugar } \\ \text { Shortening } \\ \text { Milk } \end{array} \right] \left[ \begin{array} { l l } 4 & 5 \\ 7 & 10 \\ 12 & 12 \\ 15 & 16 \\ 4 & 6 \end{array} \right] = B atrix multiplication to find a matrix giving the comparative cost per item for the two purchase options. Give each Cost to the nearest cent.](https://storage.examlex.com/TB6590/11eb4038_b0c7_eb05_ad6e_33ecd561e7c2_TB6590_00.jpg) The cost (in cents) per unit of ingredient when purchased in large lots or small lots is given in matrix B.
Use m Cost
Large Lot Small Lot
atrix multiplication to find a matrix giving the comparative cost per item for the two purchase options. Give each Cost to the nearest cent.
The cost (in cents) per unit of ingredient when purchased in large lots or small lots is given in matrix B.
Use m Cost
Large Lot Small Lot
atrix multiplication to find a matrix giving the comparative cost per item for the two purchase options. Give each Cost to the nearest cent.
(Multiple Choice)
4.8/5  (28)
(28)
Some people must eat a low-sodium diet with no more than 2000 mg of sodium per day. By eating 1 cracker, 1 pretzel, and 1 cookie, a person would ingest 149 mg of sodium. If a person ate 8 pretzels and 8 cookies, he or she
Would ingest 936 mg of sodium. By eating 6 crackers and 7 pretzels, a person would take in 535 mg of sodium.
Which of the following statements is true?
(Multiple Choice)
4.8/5  (43)
(43)
A matrix has an inverse if and only if its determinant does not equal 0. Determine whether the given matrix has an
inverse.
-
(Multiple Choice)
4.7/5  (22)
(22)
Use an inverse matrix to find the solution to the system.
-A trucking company has an order for two products, A and B, to be delivered to a store. The table below gives the volume and weight for each unit of the products. Product A Product B Unit Volume (cu ft) 47 68 Unit Weight (lb) 351 376 If the truck that can deliver the products can carry 4501 cu ft and 28,077 lb, how many units of each product can the
Truck carry?
(Multiple Choice)
4.8/5  (30)
(30)
Solve using Cramer's Rule.
-The sum of a student's three scores is 230. If the first is 22 points more than the second, and the sum of the first two is 14 more than twice the third, what was the first score?
(Multiple Choice)
4.8/5  (38)
(38)
A young woman wins $150,000 and buys 5 new cars. She chooses from cars that are priced at $40,000, $30,000, and $25,000 and spends all of the money. How many $25,000 cars did she buy?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the system graphically.
-The volume of a cube is given by . What is the area of each side of the cube?
(Multiple Choice)
4.9/5  (42)
(42)
Showing 101 - 120 of 196
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)