Exam 8: Systems of Equations and Inequalities
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Solve Problems Using Systems of Linear Equations
-One number is 8 less than a second number. Twice the second number is 61 more than 5 times the first. Find the two numbers.
(Multiple Choice)
4.9/5  (45)
(45)
Graph the solution set of the system of inequalities or indicate that the system has no solution.
- y\geq y\leq8
(Multiple Choice)
5.0/5  (38)
(38)
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
- +=1 -=0
(Multiple Choice)
4.7/5  (32)
(32)
Graph the solution set of the system of inequalities or indicate that the system has no solution.
-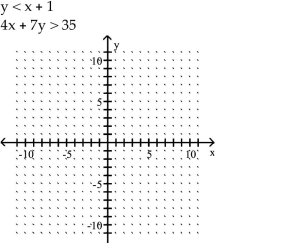
(Multiple Choice)
4.9/5  (31)
(31)
Decompose P/Q, Where Q Has a Prime, Repeated Quadratic Factor
-
(Multiple Choice)
4.7/5  (40)
(40)
Use Linear Programming to Solve Problems
-A vineyard produces two special wines, a white and a red. A bottle of the white wine requires 14 pounds of grapes and 1 hour of processing time. A bottle of red wine requires 25 pounds of grapes and 2 hours of processing time. The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing time to the production of these wines. A bottle of the white wine sells for , while a bottle of the red wine sells for . How many bottles of each type should the vineyard produce in order to maximize gross sales?
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the given ordered pair is a solution of the system.
- (-3,3) 4x-y=-9 2x+4y=6
(Multiple Choice)
4.8/5  (29)
(29)
Write the partial fraction decomposition of the rational expression.
-
(Multiple Choice)
5.0/5  (39)
(39)
Systems of Linear Equations in Three Variables
1 Verify the Solution of a System of Linear Equations in Three Variables
- (-2,-5,0) x-y+2z=1 4x+z=-2 x+2y+z=-12
(Multiple Choice)
4.9/5  (32)
(32)
Graph the solution set of the system of inequalities or indicate that the system has no solution.
- 3x-y\leq-6 x+3y\geq6
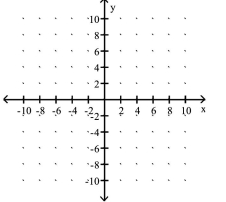
(Multiple Choice)
4.8/5  (34)
(34)
Solve Problems Using Systems of Linear Equations
-A bank teller has and bills in her cash drawer. The value of the bills is . How many bills are there?
(Multiple Choice)
4.9/5  (40)
(40)
Solve Problems Using Systems of Nonlinear Equations
-The difference between the squares of two numbers is 108 . Twice the square of the second number subtracted from the square of the first number is 72 . Find the numbers.
(Multiple Choice)
4.8/5  (41)
(41)
Solve Linear Systems by Substitution
- x+8y=-49 -4x+7y=-77
(Multiple Choice)
4.9/5  (29)
(29)
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
- x+y=5 x+y=-4
(Multiple Choice)
4.8/5  (31)
(31)
Solve Problems Using Systems of Nonlinear Equations
-A person at the top of a 600 foot tall building drops a yellow ball. The height of the yellow ball is given by the equation where is measured in feet and is the number of seconds since the yellow ball was dropped. A second person, in the same building but on a lower floor that is 264 feet from the ground, drops a white ball 3 seconds after the yellow ball was dropped. The height of the white ball is given by the equation where is measured in feet and is the number of seconds since the yellow ball was dropped. Find the time that the balls are the same distance above the ground and find this distance.
(Multiple Choice)
4.9/5  (38)
(38)
Showing 141 - 160 of 288
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)