Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Graph the function.
-Use the graph of to obtain the graph of .
(Multiple Choice)
4.8/5  (30)
(30)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
5.0/5  (37)
(37)
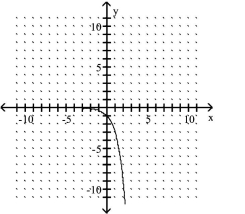
The graph of an exponential function is given. Select the function for the graph from the functions listed.
-
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-The population of a certain country is growing at a rate of per year. How long will it take for this country's population to double? Use the formula , which gives the time, , for a population with growth rate k, to double. (Round to the nearest whole year.)
(Multiple Choice)
4.9/5  (40)
(40)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
4.8/5  (28)
(28)
Solve the exponential equation. Express the solution set in terms of natural logarithms.
-
(Multiple Choice)
4.8/5  (37)
(37)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (40)
(40)
Use common logarithms or natural logarithms and a calculator to evaluate to four decimal places
-Use the mathematical model for power gain, , where is the output power in watts and is the input power in watts. Determine the power gain , in decibels, for an amplifier with an output of 21 watts and an input of watts. Round to five decimal places if necessary.
(Multiple Choice)
4.8/5  (34)
(34)
Solve.
-An endangered species of fish has a population that is decreasing exponentially . The population 6 years ago was 1500 . Today, only 900 of the fish are alive. Once the population drops below 100 , the situation will be irreversible. When will this happen, according to the model? (Round to the nearest whole year.)
(Multiple Choice)
4.8/5  (30)
(30)
Graph the function.
-Use the graph of to obtain the graph of .
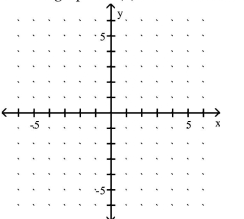
(Multiple Choice)
4.9/5  (30)
(30)
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.9/5  (33)
(33)
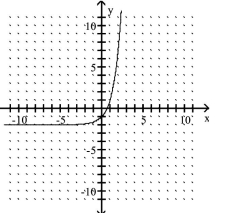
The graph of an exponential function is given. Select the function for the graph from the functions listed.
-
(Multiple Choice)
4.8/5  (34)
(34)
Use the compound interest formulas A
-Suppose that you have $4000 to invest. Which investment yields the greater return over 10 years: 6.25% compounded continuously or 6.3% compounded semiannually?
(Multiple Choice)
5.0/5  (21)
(21)
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.9/5  (41)
(41)
Approximate the number using a calculator. Round your answer to three decimal places.
-The function can be used to determine the milligrams of a certain drug in a patient's bloodstream h hours after the drug has been given. How many milligrams (to two decimals) will be present after 7 hours?
(Multiple Choice)
4.8/5  (26)
(26)
Solve the problem.
-The pH of a solution ranges from 0 to 14. An acid has a pH less than 7 . Pure water is neutral and has a pH of 7 . The of a solution is given by where represents the concentration of the hydrogen ions in the solution in moles per liter. Find the hydrogen ion concentration if the .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.8/5  (39)
(39)
Approximate the number using a calculator. Round your answer to three decimal places.
-
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)