Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Graph the function
-Use the graph of to obtain the graph of .
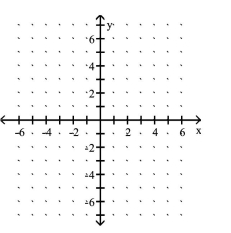
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-Cindy will require in 2 years to return to college to get an MBA degree. How much money should she ask her parents for now so that, if she invests it at compounded continuously, she will have enough for school? (Round your answer to the nearest dollar.)
(Multiple Choice)
4.9/5  (24)
(24)
Approximate the number using a calculator. Round your answer to three decimal places.
-
(Multiple Choice)
4.9/5  (29)
(29)
Evaluate the expression without using a calculator.
-The function models the average number of free-throws a basketball player can make consecutively during practice as a function of time, where is the number of consecutive days the basketball player has practiced for two hours. After 147 days of practice, what is the average number of consecutive free throws the basketball player makes?
(Multiple Choice)
4.7/5  (29)
(29)
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-
(Multiple Choice)
4.9/5  (32)
(32)
Use the compound interest formulas A
-Find the accumulated value of an investment of $5000 at 5% compounded monthly for 8 years.
(Multiple Choice)
4.7/5  (33)
(33)
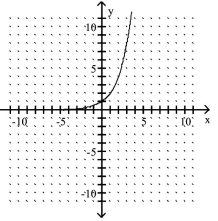
The graph of an exponential function is given. Select the function for the graph from the functions listed.
-
(Multiple Choice)
4.8/5  (28)
(28)
Solve the equation by expressing each side as a power of the same base and then equating exponents.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the logarithmic equation. Be sure to reject any value that is not in the domain of the original logarithmic
expressions. Give the exact answer.
-
(Multiple Choice)
4.8/5  (30)
(30)
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm
whose coefficient is 1. Where possible, evaluate logarithmic expressions.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the equation by expressing each side as a power of the same base and then equating exponents.
-
(Multiple Choice)
5.0/5  (34)
(34)
Approximate the number using a calculator. Round your answer to three decimal places.
-
(Multiple Choice)
4.7/5  (40)
(40)
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-
(Multiple Choice)
4.7/5  (37)
(37)
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-
(Multiple Choice)
4.8/5  (39)
(39)
Graph the function.
-Use the graph of to obtain the graph of .
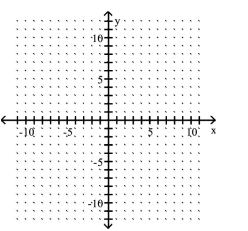
(Multiple Choice)
4.7/5  (33)
(33)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-The population of a particular country was 22 million in 1985 ; in 2000 , it was 31 million. The exponential growth function describes the population of this country t years after 1985 . Use the fact that 15 years after 1985 the population increased by 9 million to find to three decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Showing 141 - 160 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)