Exam 3: Polynomial and Rational Functions
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Determine the constant of variation for the stated condition.
-If varies directly as the cube of , and when , find when .
(Multiple Choice)
4.9/5  (28)
(28)
Find the zeros for the polynomial function and give the multiplicity for each zero. State whether the graph crosses
the x-axis or touches the x-axis and turns around, at each zero.
-Crosses the -axis at , and 4 ; lies below the -axis between and 0 ; lies above the -axis between 0 and
(Multiple Choice)
4.9/5  (40)
(40)
Find the zeros for the polynomial function and give the multiplicity for each zero. State whether the graph crosses
the x-axis or touches the x-axis and turns around, at each zero.
-
(Multiple Choice)
4.9/5  (37)
(37)
Determine the maximum possible number of turning points for the graph of the function.
-
(Multiple Choice)
4.9/5  (38)
(38)
Find the indicated intercept(s) of the graph of the function.
- -intercepts of
(Multiple Choice)
4.8/5  (36)
(36)
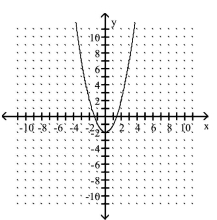
The graph of a quadratic function is given. Determine the function's equation.
-
(Multiple Choice)
4.8/5  (43)
(43)
Use the graph or table to determine a solution of the equation. Use synthetic division to verify that this number is a
solution of the equation. Then solve the polynomial equation.
-
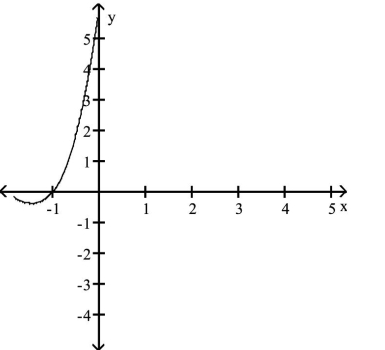
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-The revenue achieved by selling x graphing calculators is figured to be x(42 - 0.5x) dollars. The cost of each calculator is $22. How many graphing calculators must be sold to make a profit (revenue - cost) of at least $182.00?
(Multiple Choice)
4.8/5  (48)
(48)
Determine the constant of variation for the stated condition.
- varies directly as and when . Find when .
(Multiple Choice)
4.9/5  (37)
(37)
Write an equation that expresses the relationship. Use k as the constant of variation.
-a varies inversely as the square of .
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the function is a polynomial function.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the rational inequality and graph the solution set on a real number line. Express the solution set in interval
notation.
-
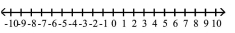
(Multiple Choice)
4.9/5  (37)
(37)
Write an equation that expresses the relationship. Use k as the constant of variation.
-If the force acting on an object stays the same, then the acceleration of the object is inversely proportional to its mass. If an object with a mass of 15 kilograms accelerates at a rate of 2 meters per second per second by a force, find the rate of acceleration of an object with a mass of 3 kilograms that is pulled by the same force.
(Multiple Choice)
4.9/5  (36)
(36)
Use transformations of f(x) to graph the rational function.
-
(Multiple Choice)
4.7/5  (42)
(42)
Find the x-intercepts (if any) for the graph of the quadratic function.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the x-intercepts (if any) for the graph of the quadratic function.
-
(Multiple Choice)
5.0/5  (44)
(44)
Determine whether the function is a polynomial function.
-
(Multiple Choice)
4.7/5  (36)
(36)
Showing 301 - 320 of 532
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)