Exam 3: Polynomial and Rational Functions
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Find the domain and range of the quadratic function whose graph is described.
-The vertex is (-1, -12) and the graph opens up.
(Multiple Choice)
5.0/5  (48)
(48)
Determine the constant of variation for the stated condition.
-The power that a resistor must dissipate is jointly proportional to the square of the current flowing through the resistor and the resistance of the resistor. If a resistor needs to dissipate 28 watts of power when 2 amperes of current is flowing through the resistor whose resistance is 7 ohms, find the power that a resistor needs to dissipate when 3 amperes of current are flowing through a resistor whose resistance is 7 ohms.
(Multiple Choice)
4.9/5  (38)
(38)
Find the indicated intercept(s) of the graph of the function.
- -intercepts of
(Multiple Choice)
4.7/5  (35)
(35)
Find the slant asymptote, if any, of the graph of the rational function.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The profit that the vendor makes per day by selling pretzels is given by the function . Find the number of pretzels that must be sold to maximize profit.
(Multiple Choice)
4.8/5  (28)
(28)
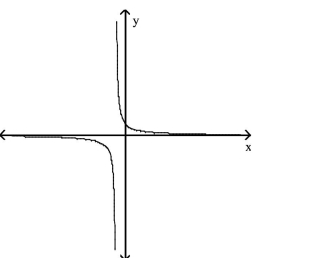
Determine whether the graph shown is the graph of a polynomial function.
-
(Multiple Choice)
4.8/5  (26)
(26)
Use the Leading Coefficient Test to determine the end behavior of the polynomial function. Then use this end
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A rectangular playground is to be fenced off and divided in two by another fence parallel to one side of the playground. 528 feet of fencing is used. Find the dimensions of the playground that maximize the total enclosed area.
(Multiple Choice)
4.9/5  (40)
(40)
Find a rational zero of the polynomial function and use it to find all the zeros of the function.
-
(Multiple Choice)
4.9/5  (40)
(40)
Write an equation that expresses the relationship. Use k as the constant of variation.
- varies inversely as , and when . Find when .
(Multiple Choice)
4.7/5  (34)
(34)
Find the zeros for the polynomial function and give the multiplicity for each zero. State whether the graph crosses
the x-axis or touches the x-axis and turns around, at each zero.
-Touches the -axis at 0 and crosses the -axis at 2 ; lies below the -axis between 0 and 2 .
(Multiple Choice)
4.8/5  (44)
(44)
Determine whether the given quadratic function has a minimum value or maximum value. Then find the
coordinates of the minimum or maximum point.
-
(Multiple Choice)
4.8/5  (30)
(30)
Determine the constant of variation for the stated condition.
- when
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the function is a polynomial function.
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-A company that produces computer printers has costs given by the function , where is the number of computer printers manufactured and is measured in dollars. The average cost to manufacture each computer printer is given by
Find . (Round to the nearest dollar, if necessary.)
(Multiple Choice)
4.7/5  (49)
(49)
Solve the polynomial inequality and graph the solution set on a number line. Express the solution set in interval
notation.
-
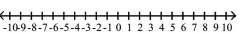
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-You have 136 feet of fencing to enclose a rectangular region. Find the dimensions of the rectangle that maximize the enclosed area.
(Multiple Choice)
4.9/5  (39)
(39)
Showing 481 - 500 of 532
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)