Exam 9: Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses

We are interested in comparing the average supermarket prices of two leading colas. Our sample was taken by randomly selecting eight supermarkets and recording the price of a six-pack of each brand of cola at each supermarket. The data are shown in the following table: Price Supermarket Brand 1 Brand 2 Difference 1 \ 2.25 \ 2.30 \- 0.05 2 2.47 2.45 0.02 3 2.38 2.44 -0.06 4 2.27 2.29 -0.02 5 2.15 2.25 -0.10 6 2.25 2.25 0.00 7 2.36 2.42 -0.06 8 2.37 2.40 -0.03 =2.3125 =2.3500 =-0.0375 =0.1007 =0.0859 =0.0381 Find a $98 \%$ confidence interval for the difference in mean price of brand 1 and brand 2 . A) $0.0375 \pm 0.0404$ B) $0.0375 \pm 0.1393$ C) $0.0375 \pm 0.0471$ D) $0.0375 \pm 0.0347$

Two surgical procedures are widely used to treat a certain type of cancer. To compare the success rates of the two procedures, random samples of surgical patients were obtained and the numbers of patients who showed no recurrence of the disease after a 1-year period were recorded. The data are shown in the table. n Number of Successes Procedure A 100 83 Procedure B 100 81 How large a sample would be necessary in order to estimate the difference in the true success rates to within .10 with 95% reliability?

The screen below shows the $95 \%$ confidence interval for 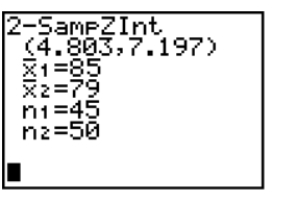$\left( \mu _ { 1 } - \mu _ { 2 } \right)$ . What does the interval suggest about the relationship between $\mu _ { 1 }$ and $\mu _ { 2 }$ ?

Independent random samples were selected from each of two normally distributed populations, n1 = 7 from population 1 and n2 = 9 from population 2. The data are shown below. Population 1: 2.5 3.1 2.3 1.8 4.2 3.5 3.9 Population 2: 2.9 1.7 4.6 3.5 3.7 2.8 4.6 3.4 1.9 Find the test statistic for the test of $H _ { 0 } : \sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 }$ against $H _ { a } : \sigma _ { 1 } ^ { 2 } \neq \sigma _ { 2 } ^ { 2 }$ .

When blood levels are low at an area hospital, a call goes out to local residents to give blood. The blood center is interested in determining which sex - males or females - is more likely to respond. Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes between the male and female responses. What type of analysis should be used?

An experiment has been conducted at a university to compare the mean number of study hours expended per week by student athletes with the mean number of hours expended by non athletes. A random sample of 55 athletes produced a mean equal to 20.6 hours studied per week and a standard deviation equal to 5.3 hours. A second random sample of 200 non athletes produced a mean equal to 23.5 hours per week and a standard deviation equal to 4.3 hours. How many students would need to be sampled in order to estimate the difference in means to within 1.5 hours with probability 95%?

The FDA is comparing the mean caffeine contents of two brands of cola. Independent random samples of 6 -oz. cans of each brand were selected and the caffeine content of each can determined. The study provided the following summary information. Brand A Brand B Sample size 15 10 Mean 18 20 Variance 1.2 1.5 How many cans of each soda would need to be sampled in order to estimate the difference in the mean caffeine content to within. 10 with $90 \%$ reliability? A) $n _ { 1 } = n _ { 2 } = 731$ B) $n _ { 1 } = n _ { 2 } = 1038$ C) $n _ { 1 } = n _ { 2 } = 74$ D) $n _ { 1 } = n _ { 2 } = 104$

Independent random samples of 100 observations each are chosen from two normal populations with the following means and standard deviations. Population 1 Population 2 Population 1 Population 2 =15 =13 =3 =2 Find the mean and standard deviation of the sampling distribution of $\left( \bar { x } _ { 1 } - \bar { x } _ { 2 } \right)$ .

Independent random samples selected from two normal populations produced the following sample means and standard deviations. Sample 1 Sample 2 =14 =11 =7.1 =8.4 =2.3 =2.9 Conduct the test : - =0 against. : - 0 , Use \alpha=.05 .

The owners of an industrial plant want to determine which of two types of fuel (gas or electricity) will produce more useful energy at a lower cost. The cost is measured by plant investment per delivered quad ($ invested /quadrillion BTUs). The smaller this number, the less the industrial plant pays for delivered energy. Random samples of 11 similar plants using electricity and 16 similar plants using gas were taken, and the plant investment/quad was calculated for each. In an analysis of the difference of means of the two samples, the owners were able to reject H0 in the test H0: (μE - μG) = 0 vs. Ha: (μE - μG) > 0. What is our best interpretation of the result?

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 Calculate the appropriate test statistic for a test about $\mu _ { 1 } - \mu _ { 2 }$ . A) $z = - 2.28$ B) $z = - 2.45$ C) $z = - 2.81$ D) $z = - 3.02$

We sampled 100 men and 100 women and asked: "Do you think the environment is a major concern?" Of those sampled, 67 women and 53 men responded that they believed it is. For the confidence interval procedure to work properly, what additional assumptions must be satisfied?

Given $v _ { 1 } = 9 \text { and } v _ { 2 } = 5 \text {, find } P ( F > 6.68 )$

Specify the appropriate rejection region for testing $\mathrm { H } _ { 0 : } : \sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 }$ in the given situation. - $\mathrm { H } _ { \mathrm { a } } : \sigma _ { 1 } ^ { 2 } \neq \sigma _ { 2 } ^ { 2 } ; \alpha = 0.10 , \mathrm { n } _ { 1 } = 10 , \mathrm { n } _ { 2 } = 16$ Assume that $s _ { 2 } ^ { 2 } > s _ { 1 } ^ { 2 }$ . A) $F > 3.01$ B) $F > 2.59$ C) $| \mathrm { F } | > 2.34$ D) $| \mathrm { F } | > 2.59$ 9 Identify the rejection region that should be used to test $H _ { 0 } : \sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 }$ against $H _ { \mathrm { a } } : \sigma _ { 1 } ^ { 2 } \approx \sigma _ { 2 } ^ { 2 }$ for $v _ { 1 } = 5 , v _ { 2 } = 8$ , and $\alpha = .05$ . A) $F > 4.82$ B) $F > 3.69$ C) $F > 6.76$ D) $F > 6.63$ 10 Identify the rejection region that should be used to test $H _ { 0 } : \sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 }$ against $H _ { a } : \sigma _ { 1 } { } ^ { 2 } > \sigma _ { 2 } ^ { 2 }$ for $v _ { 1 } = 10$ , v $v _ { 2 } = 29$ , and $\alpha = .10$ . A) $F > 1.83$ B) $F > 2.18$ C) $F > 2.53$ D) $F > 3.00$