Exam 5: Continuous Random Variables

If a data set is normally distributed, what is the proportion of measurements you would expect to fall within μ ± σ?

A machine is set to pump cleanser into a process at the rate of 5 gallons per minute. Upon inspection, it is learned that the machine actually pumps cleanser at a rate described by the uniform distribution over the interval 4.5 to 7.5 gallons per minute. Find the variance of the distribution.

The exponential distribution is governed by two quantities, μ and σ, that determine its shape and location

The diameters of ball bearings produced in a manufacturing process can be described using a uniform distribution over the interval 6.5 to 8.5 millimeters. What is the mean diameter of ball bearings produced in this manufacturing process?

A physical fitness association is including the mile run in its secondary-school fitness test. The time for this event for boys in secondary school is known to possess a normal distribution with a mean of 440 seconds and a standard deviation of 50 seconds. Find the probability that a randomly selected boy in secondary school can run the mile in less than 325 seconds.

The printout below contains summary statistics of the heights of a sample of 200 adult men in the United States. Descriptive Statistics: HT Variable N Mean StDev Minimum Q1 Median Q2 Maximum HT 200 70.187 2.716 62.375 67.875 69.625 71.500 91.125 Use the information in the printout to determine whether the distribution of heights is approximately normal. Explain your reasoning.

Farmers often sell fruits and vegetables at roadside stands during the summer. One such roadside stand has a daily demand for tomatoes that is approximately normally distributed with a mean of 405 tomatoes and a standard deviation of 30 tomatoes. If there are 363 tomatoes available to be sold at the roadside stand at the beginning of a day, what is the probability that they will all be sold?

The length of time (in months) that a cashier works for a certain fast food restaurant is exponentially distributed with a mean of 7 months. a. Find the probability that a cashier works for the restaurant for at least 2 years. b. Find the probability that a cashier works for the restaurant for less than 1 month.

The diameters of ball bearings produced in a manufacturing process can be described using a uniform distribution over the interval 2.5 to 4.5 millimeters. Any ball bearing with a diameter of over 4.25 millimeters or under 2.75 millimeters is considered defective. What is the probability that a randomly selected ball bearing is defective?

Before a new phone system was installed, the amount a company spent on personal calls followed a normal distribution with an average of $500 per month and a standard deviation of $50 per month. Refer to such expenses as PCE's (personal call expenses). Find the point in the distribution below which 2.5% of the PCE's fell.

Assume that x is a binomial random variable with n = 100 and p = 0.60. Use a normal approximation to find P(x < 65).

A physical fitness association is including the mile run in its secondary-school fitness test. The time for this event for boys in secondary school is known to possess a normal distribution with a mean of 460 seconds and a standard deviation of 40 seconds. The fitness association wants to recognize the fastest 10% of the boys with certificates of recognition. What time would the boys need to beat in order to earn a certificate of recognition from the fitness association?

The board of examiners that administers the real estate broker's examination in a certain state found that the mean score on the test was 419 and the standard deviation was 72. If the board wants to set the passing score so that only the best 80% of all applicants pass, what is the passing score? Assume that the scores are normally distributed.

Which one of the following suggests that the data set is not approximately normal? A) A data set with $68 \%$ of the measurements within $\bar { x } \pm 2 \mathrm {~s}$ . B) 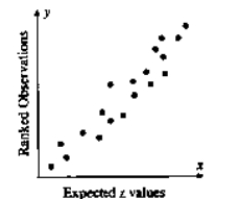C) Stem Leaves 3 0 3 9 4 2 4 7 7 5 1 3 4 8 8 9 9 9 6 0 0 5 6 6 7 8 7 1 1 5 8 2 7 D) A data set with $\mathrm { IQR } = 752$ and $s = 574$ .

You are performing a study about the weight of preschoolers. A previous study found the weights to be normally distributed with a mean of 30 pounds and a standard deviation of 4 pounds. You randomly sample 30 preschool children and find their weights (in pounds) to be as follows. 25 25 26 26.5 27 27 27.5 28 28 28.5 29 29 30 30 30.5 31 31 32 32.5 32.5 33 33 34 34.5 35 35 37 37 38 38 Draw a histogram to display the data. Is it reasonable to assume that the weights are normally distributed? Why?

Suppose that x has an exponential distribution with $\theta = 5 . \text { Find } P ( x \leq 10 )$

High temperatures in a certain city for the month of August follow a uniform distribution over the interval 68°F to 90°F. What is the probability that the high temperature on a day in August exceeds 73°F?

Suppose x is a random variable best described by a uniform probability distribution with c = 6 and d = 14. Find the value of a that makes the following probability statement true: P(x ≥ a) = 0.6.

Suppose x is a random variable best described by a uniform probability distribution with c = 30 and d = 90. Find P(30 ≤ x ≤ 45).

The time between arrivals at an ATM machine follows an exponential distribution with θ = 10 minutes. Find the mean and standard deviation of this distribution.