Exam 12: Congruence and Similarity With Constructions
Exam 1: An Introduction to Problem Solving85 Questions
Exam 2: Introduction to Logic and Sets153 Questions
Exam 3: Numeration Systems and Whole Number Operations194 Questions
Exam 4: Number Theory116 Questions
Exam 5: Integers122 Questions
Exam 6: Rational Numbers and Proportional Reasoning85 Questions
Exam 7: Rational Numbers As Decimals and Percents102 Questions
Exam 8: Real Numbers and Algebraic Thinking151 Questions
Exam 9: Probability129 Questions
Exam 10: Data Analysisstatistics: an Introduction57 Questions
Exam 11: Introductory Geometry115 Questions
Exam 12: Congruence and Similarity With Constructions121 Questions
Exam 13: Congruence and Similarity With Transformations56 Questions
Exam 14: Area, Pythagorean Theorem, and Volume124 Questions
Select questions type
Solve.
-Explain how to construct a parallelogram given two adjacent sides. If it is not possible, explain why.
(Essay)
4.8/5  (34)
(34)
Answer the question.
-A quadrilateral is a______ if and only if opposite sides are parallel or congruent.
(Short Answer)
4.9/5  (32)
(32)
Solve.
-Describe how to draw a square so that a given circle circumscribes the square.
(Essay)
4.7/5  (30)
(30)
Use a ruler, protractor, and compass to construct, if possible, a triangle with the stated properties. If such a triangle cannot be drawn, explain why. Decide if there can be two or more noncongruent triangles with the stated properties.
-A triangle with sides of length 19 cm, 9 cm, and 26 cm
(Multiple Choice)
4.8/5  (42)
(42)
Provide the requested proof.
-Suppose polygon is any square with diagonals and intersecting at point .
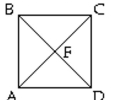 What can be said about any point on and points and ?
What can be said about any point on and points and ?
(Essay)
4.9/5  (28)
(28)
State whether the triangles are congruent. If the information given is not sufficient, state "No conclusion possible".
-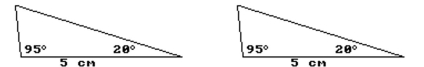
(Multiple Choice)
4.8/5  (27)
(27)
Answer the question.
-A tree casts a shadow 40 meters long. At the same time, the shadow cast by a vertical 5 meter stick is 10 meters long. Find the height of the tree.
(Multiple Choice)
4.8/5  (30)
(30)
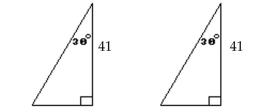
State whether the triangles are congruent. If the information given is not sufficient, state "No conclusion possible".
-
(Multiple Choice)
4.8/5  (37)
(37)
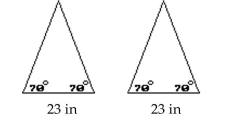
State whether the triangles are congruent. If the information given is not sufficient, state "No conclusion possible".
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve.
-Given a right triangle ABC, explain how to construct an altitude from vertex A. 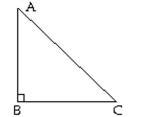
(Essay)
4.8/5  (33)
(33)
Solve.
-Given , construct the perpendicular bisector of without putting any marks below .

(Essay)
4.8/5  (38)
(38)
Solve.
-Explain how to construct a triangle with two obtuse angles. If it is not possible, explain why.
(Essay)
4.8/5  (37)
(37)
Answer the question.
-What type of figure is formed by joining the midpoints of the adjacent sides of a rectangle?
(Short Answer)
4.8/5  (32)
(32)
A sector of a circle is a pie-shaped section bounded by two radii and an arc. What is a
minimal set of conditions for determining that two sectors of the same circle are congruent?
(Essay)
4.8/5  (29)
(29)
Answer the question.
-Are two regular pentagons always similar? Explain why or why not.
(Essay)
4.8/5  (32)
(32)
Showing 61 - 80 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)