Exam 10: Counting Methods
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Solve the problem.
-Find the number of three member committees that could be selected from the group of {Mary, Norman, Paula, Raymond, Sally} given that all club members are eligible to be members of the
Committee.
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-A class has 10 boys and 12 girls. In how many ways can a committee of four be selected if the committee can have at most two girls?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-If a license plate consists of two letters followed by four digits, how many different licenses could be created having at least one letter or digit repeated.
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-Construct a product table showing all possible two-digit numbers using digits from the set {1, 2, 6, 7}. List the even numbers in the table.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-In how many ways can the letters in the word PAYMENT be arranged if the letters are taken 5 at a time?
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-A sports shop sold tennis rackets in 3 different weights, 3 types of string, and 4 grip sizes. How many different rackets could be sold?
(Multiple Choice)
4.7/5  (35)
(35)
Complete the magic (addition)square. A magic square has the property that the sum of the numbers in any row, column, or diagonal is the same.
-Use each number 33, 34, 35, 36, 37, 38, 39, 40, and 41 once.
35 36 37 41 34
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A musician plans to perform 5 selections for a concert. If he can choose from 9 different selections, how many ways can he arrange his program?
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-How many odd three-digit numbers can be written using digits from the set if no digit may be used more than once?
(Multiple Choice)
4.8/5  (36)
(36)
Given a magic square, other magic squares may be obtained by rotating, adding, or subtracting a constant value to or from each entry, multiplying each entry by a constant, or dividing each entry by a nonzero constant. Start with the given magic square and perform the indicated operation to find a new magic square.
-Subtract 7
9 16 11 14 12 10 13 8 15
(Multiple Choice)
4.9/5  (29)
(29)
How many different three-digit numbers can be written using digits from the set without any repeating digits?
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-How many five-digit counting numbers contain at least one 6?
(Multiple Choice)
4.7/5  (44)
(44)
Determine the number of figures (of any size)in the design.
-Cubes (of any size)
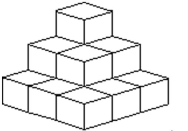
(Multiple Choice)
4.8/5  (38)
(38)
Given a magic square, other magic squares may be obtained by rotating, adding, or subtracting a constant value to or from each entry, multiplying each entry by a constant, or dividing each entry by a nonzero constant. Start with the given magic square and perform the indicated operation to find a new magic square.
-Multiply by 4 8 1 6 3 5 7 4 9 2
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Construct a product table showing all possible two-digit numbers using digits from the set {1, 2, 6, 7}. List the square numbers in the table.
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-A pool of possible jurors consists of 10 men and 16 women. How many different juries consisting of 5 men and 7 women are possible?
(Multiple Choice)
4.8/5  (33)
(33)
Complete the magic (addition)square. A magic square has the property that the sum of the numbers in any row, column, or diagonal is the same.
-Use each number 4, 5, 6, 7, 8, 9, 10, 11, and 12 once.
7 6 8 11 4 9
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Given a group of students: Allen, Brenda, Chad, Dorothy, Eric, Frances, Gale , count the number of different ways of choosing 4 people for a committee. Assume no one can hold more than one office and that each person is to hold a different position on the committee.
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Consider all the subsets of {r, s, t, u, v, x}. How many of them have 3 elements?
(Multiple Choice)
4.7/5  (42)
(42)
Solve the problem.
-If a given set has thirteen elements, how many of its subsets have somewhere from four through eight elements?
(Multiple Choice)
4.8/5  (28)
(28)
Showing 101 - 120 of 213
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)