Exam 1: The Art of Problem Solving
Exam 1: The Art of Problem Solving190 Questions
Exam 2: The Basic Concepts of Set Theory316 Questions
Exam 3: Introduction to Logic315 Questions
Exam 4: Numeration Systems245 Questions
Exam 5: Number Theory171 Questions
Exam 6: The Real Numbers and Their Representations401 Questions
Exam 7: The Basic Concepts of Algebra273 Questions
Exam 8: Graphs, Functions, and Systems of Equations and Inequalities136 Questions
Exam 9: Geometry182 Questions
Exam 10: Counting Methods213 Questions
Exam 11: Probability140 Questions
Exam 12: Statistics152 Questions
Exam 13: Personal Financial Management260 Questions
Exam 14: Trigonometry Formerly234 Questions
Exam 15: Graph Theory110 Questions
Exam 16: Voting and Apportionment99 Questions
Select questions type
Use inductive reasoning to predict the next equation.
-(1 × 9)- 7 = 2
(21 × 9)- 7 = 182
(321 × 9)- 7 = 2882
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-An average library contains at least 50 and at most 250 books. How many library owners must be polled to be certain that at least two owners have the same number of books in their libraries?
(Multiple Choice)
4.7/5  (33)
(33)
Use logic to solve the problem.
-If it takes 10 minutes to hard-boil 5 goose eggs when dropped into boiling water, how long will it take to hard-boil 10 goose eggs?
(Short Answer)
4.9/5  (31)
(31)
Use your calculator to perform the indicated operations. Give as many digits in your answer as shown on your calculator display.
-41.3 - 7 × 4.5
(Multiple Choice)
4.9/5  (48)
(48)
Complete the magic (addition)square. A magic square has the property that the sum of the numbers in any row, column,
or diagonal is the same.
-Use each number 8, 9, 10, 11, 12, 13, 14, 15, and 16 once.
11 9 12 14 8
(Multiple Choice)
4.7/5  (38)
(38)
Use the indicated formula to find the sum.
-Use to find the sum of
(Multiple Choice)
4.8/5  (32)
(32)
Use logic to solve the problem.
-Mike and Tom find a long drainage pipe in a vacant lot. It is big enough so that each boy can just manage to squeeze into it and crawl from one end to the other. If Mike and Tom go into the pipe from opposite ends, is it possible for each boy to crawl the entire length of the pipe and come out the other end?
(Essay)
4.9/5  (43)
(43)
Find a pattern and use it to solve the problem.
-Find the next term: 2, 3, 5, 7, 11, 13
(Multiple Choice)
4.9/5  (38)
(38)
Determine the number of figures (of any size)in the design.
-Squares (of any size)
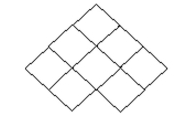
(Multiple Choice)
4.7/5  (30)
(30)
Use the indicated formula to find the sum.
-Use to find the sum of .
(Multiple Choice)
4.9/5  (40)
(40)
Showing 181 - 190 of 190
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)