Exam 7: Applications of Trigonometric Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
the motion is simple harmonic with period T, write an equation that relates the displacement d of the object from its rest
position after t seconds. Also assume that the positive direction of the motion is up.An object attached to a coiled spring is pulled down a distance a from its rest position and then released. Assuming that
-a = 5; T = 10 seconds A)
B)
D)
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-A building 200 feet tall casts a 40 foot long shadow. If a person looks down from the top of the building, what is the measure of the angle between the end of the shadow and the vertical side of the building (to the nearest
Degree)? (Assume the person's eyes are level with the top of the building.)
(Multiple Choice)
4.9/5  (39)
(39)
Find the area of the triangle. If necessary, round the answer to two decimal places.
-
(Multiple Choice)
5.0/5  (34)
(34)
The displacement d (in meters) of an object at time t (in seconds) is given. Describe the motion of the object. What is the
maximum displacement from its resting position, the time required for one oscillation, and the frequency?
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Island A is 150 miles from island B. A ship captain travels 250 miles from island A and then finds that he is off course and 160 miles from island B. What angle, in degrees, must he turn through to head straight for island B?
Round the answer to two decimal places. (Hint: Be careful to properly identify which angle is the turning
Angle.)
(Multiple Choice)
4.8/5  (30)
(30)
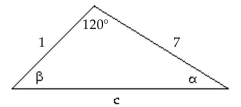
Find the area of the triangle. If necessary, round the answer to two decimal places.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-John (whose line of sight is 6 ft above horizontal) is trying to estimate the height of a tall oak tree. He first measures the angle of elevation from where he is looking as 35°. He walks 30 feet closer to the tree and finds
That the angle of elevation has increased by 12°. Estimate the height of the tree rounded to the nearest whole
Number.
(Multiple Choice)
4.8/5  (41)
(41)
Find the area of the triangle. If necessary, round the answer to two decimal places.
-a = 4, b = 5, c = 7
(Multiple Choice)
4.8/5  (32)
(32)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find cos A when a = 3 and b = 7. A)
В)
C)
D)
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-In 1838, the German mathematician and astronomer Friedrich Wilhelm Bessel was the first person to calculate
the distance to a star other than the Sun. He accomplished this by first determining the parallax of the star, 61
Cygni, at 0.314 arc seconds (Parallax is the change in position of the star measured against background stars as
Earth orbits the Sun. See illustration.) If the distance from Earth to the Sun is about 150,000,000 km and determine the distance d from Earth to 61 Cygni using Bessel's figures. 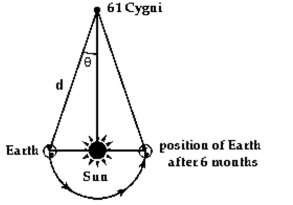
(Essay)
4.8/5  (32)
(32)
Solve the problem.
-A pier 1250 meters long extends at an angle from the shoreline. A surveyor walks to a point 1500 meters down
the shoreline from the pier and measures the angle formed by the ends of the pier. If is found to be 53°. What
acute angle (correct to the nearest 0.1°) does the pier form with the shoreline? Is there more than one possibility?
If so, how can we know which is the correct one?
(Short Answer)
5.0/5  (38)
(38)
Solve the problem.
-A box has dimensions 2" × × 4". (See illustration.)
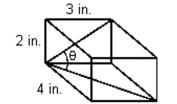 Determine the angle formed by the diagonal of the side and the diagonal of the " side. Round your answer to the nearest degree.
Determine the angle formed by the diagonal of the side and the diagonal of the " side. Round your answer to the nearest degree.
(Multiple Choice)
4.8/5  (36)
(36)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find sec when and .
(Multiple Choice)
4.8/5  (35)
(35)
Graph the damped vibration curve for 0 .
-The distance d (in meters) of the bob of a pendulum from its rest position at time t (in seconds) is given by: What is the maximum displacement of the bob after the first oscillation?
(Multiple Choice)
4.9/5  (34)
(34)
Showing 81 - 100 of 103
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)