Exam 7: Applications of Trigonometric Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
the motion is simple harmonic with period T, write an equation that relates the displacement d of the object from its rest
position after t seconds. Also assume that the positive direction of the motion is up.An object attached to a coiled spring is pulled down a distance a from its rest position and then released. Assuming that
-a = 5; T = 3 seconds A)
B)
C)
D)
(Multiple Choice)
4.9/5  (35)
(35)
Use the method of adding y-coordinates to graph the function.
-
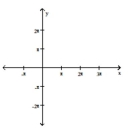 A)
A)
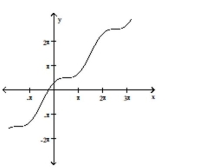 B)
B)
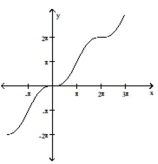 C)
C)
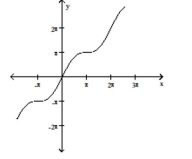 D)
D)
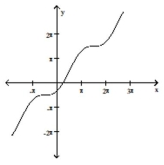
(Multiple Choice)
4.8/5  (40)
(40)
Find the area of the triangle. If necessary, round the answer to two decimal places.
-
(Multiple Choice)
5.0/5  (36)
(36)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find when and .
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The distance from home plate to dead center field in a certain baseball stadium is 402 feet. A baseball diamond is a square with a distance from home plate to first base of 90 feet. How far is it from first base to dead center
Field?
(Multiple Choice)
4.7/5  (30)
(30)
Two sides and an angle are given. Determine whether the given information results in one triangle, two triangles, or no
triangle at all. Solve any triangle(s) that results.
-
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-It is 4.7 km from Lighthouse A to Port B. The bearing of the port from the lighthouse is N73°E. A ship has sailed due west from the port and its bearing from the lighthouse is N31°E. How far has the ship sailed from the port?
Round your answer to the nearest 0.1 km.
(Multiple Choice)
4.9/5  (37)
(37)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find when and .
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-A rocket tracking station has two telescopes A and B placed 1.3 miles apart. The telescopes lock onto a rocket and transmit their angles of elevation to a computer after a rocket launch. What is the distance to the rocket
From telescope B at the moment when both tracking stations are directly east of the rocket telescope A reports an
Angle of elevation of 27° and telescope B reports an angle of elevation of 52°?
(Multiple Choice)
4.8/5  (40)
(40)
Use the method of adding y-coordinates to graph the function.
-
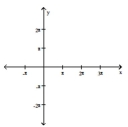 A)
A)
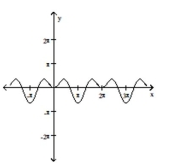 B)
B)
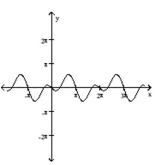 C)
C)
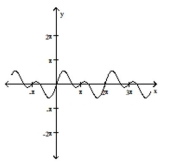 D)
D)
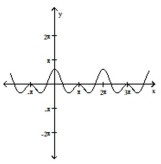
(Multiple Choice)
4.9/5  (34)
(34)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find sin B when b = 4 and c = 7. A)
B)
C)
D)
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-A surveyor standing 56 meters from the base of a building measures the angle to the top of the building and finds it to be 39°. The surveyor then measures the angle to the top of the radio tower on the building and finds
That it is 49°. How tall is the radio tower?
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Two surveyors 180 meters apart on the same side of a river measure their respective angles to a point between
them on the other side of the river and obtain 54° and 68°. How far from the point (line-of-sight distance) is
each surveyor? Round your answer to the nearest 0.1 meter.
(Short Answer)
4.7/5  (36)
(36)
Solve the problem.
-A photographer points a camera at a window in a nearby building forming an angle of 42° with the camera platform. If the camera is 52 m from the building, how high above the platform is the window, to the nearest
Hundredth of a meter?
(Multiple Choice)
4.9/5  (33)
(33)
Find the area of the triangle. If necessary, round the answer to two decimal places.
-a = 14, b = 32, c = 26
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A plane takes off from an airport on the bearing S29°W. It continues for 20 minutes then changes to bearing S52°W and flies for 2 hours 20 minutes on this course then lands at a second airport. If the plane' s speed is 420
Mph, how far from the first airport is the second airport? Round your answer correct to the nearest mile.
(Multiple Choice)
4.8/5  (36)
(36)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find sin A when a = 8 and b = 7. A)
B)
C)
D)
(Multiple Choice)
4.9/5  (32)
(32)
Showing 41 - 60 of 103
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)