Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
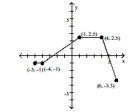
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
C
The graph of a function f is given. Use the graph to answer the question.
-Find the numbers, if any, at which f has a local maximum. What are the local maxima? 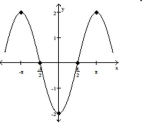 A) has a local maximum at and ; the local maximum is 2
B) f has no local maximum
C) has a local maximum at ; the local maximum is
D) has a local maximum at ; the local maximum is 2
A) has a local maximum at and ; the local maximum is 2
B) f has no local maximum
C) has a local maximum at ; the local maximum is
D) has a local maximum at ; the local maximum is 2
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
A
The graph of a piecewise-defined function is given. Write a definition for the function.
-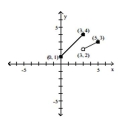 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.9/5  (43)
(43)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
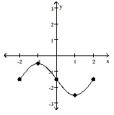
(Multiple Choice)
4.7/5  (32)
(32)
Determine whether the relation represents a function. If it is a function, state the domain and range.
-
(Multiple Choice)
4.7/5  (36)
(36)
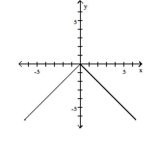
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
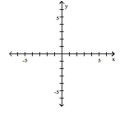 A)
A)
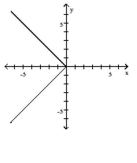 B)
B)
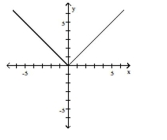 C)
C)
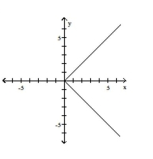 D)
D)
(Multiple Choice)
4.9/5  (40)
(40)
Find and simplify the difference quotient of f, , for the function.
-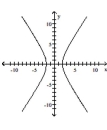 A)
function
domain: all real numbers
range: \( \{y \mid y \leq-2 \) or \( y \geq 2\} \)
intercepts: \( (-2,0),(2,0) \)
symmetry: \( y \)-axis\[\begin{array} { l l }
B)
function
domain: \( \{x \mid-2 \leq x \leq 2\} \)
range: all real numbers
intercepts: \( (-2,0),(2,0) \)
symmetry: \( \mathrm{x} \)-axis, \( y \)-axis
C)
function
domain: \( \{x \mid x \leq-2 \) or \( x \geq 2\} \)
range: all real numbers
intercepts: \( (-2,0),(2,0) \)
symmetry: \( \mathrm{x} \)-axis, \( \mathrm{y} \)-axis, origirn
D)
\(\text { not a function }\)
A)
function
domain: all real numbers
range: \( \{y \mid y \leq-2 \) or \( y \geq 2\} \)
intercepts: \( (-2,0),(2,0) \)
symmetry: \( y \)-axis\[\begin{array} { l l }
B)
function
domain: \( \{x \mid-2 \leq x \leq 2\} \)
range: all real numbers
intercepts: \( (-2,0),(2,0) \)
symmetry: \( \mathrm{x} \)-axis, \( y \)-axis
C)
function
domain: \( \{x \mid x \leq-2 \) or \( x \geq 2\} \)
range: all real numbers
intercepts: \( (-2,0),(2,0) \)
symmetry: \( \mathrm{x} \)-axis, \( \mathrm{y} \)-axis, origirn
D)
\(\text { not a function }\)
(Multiple Choice)
4.8/5  (25)
(25)
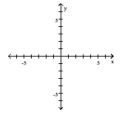
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
 A)
A)
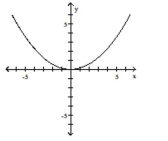 B)
B)
 C)
C)
 D)
D)
(Multiple Choice)
4.8/5  (40)
(40)
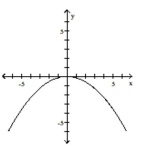
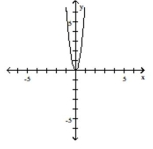
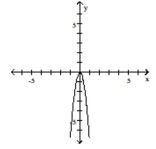
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
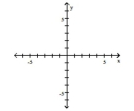 A)
A)
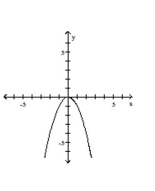 B)
B)
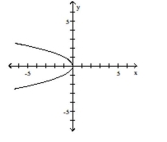 C)
C)
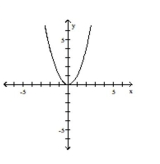 D)
D)
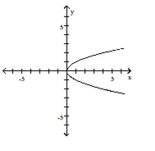
(Multiple Choice)
4.7/5  (35)
(35)
The graph of a function f is given. Use the graph to answer the question.
-Is f(3) positive or negative? 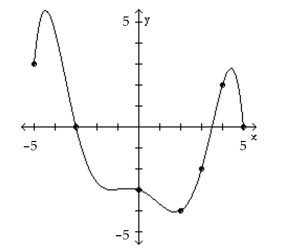
(Multiple Choice)
4.9/5  (33)
(33)
For the function, find the average rate of change of f from 1 to x:
-
(Multiple Choice)
4.9/5  (38)
(38)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
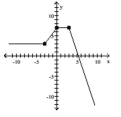
(Multiple Choice)
4.8/5  (33)
(33)
The graph of a piecewise-defined function is given. Write a definition for the function.
-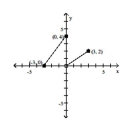 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.7/5  (32)
(32)
Choose the one alternative that best completes the statement or answers the question.
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
 A)
A)
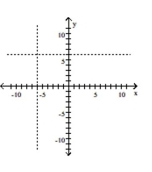 B)
B)
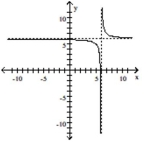 C)
C)
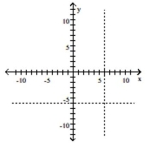 D)
D)
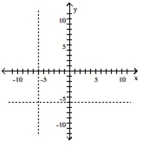
(Multiple Choice)
4.8/5  (42)
(42)
The graph of a function f is given. Use the graph to answer the question.
-What are the x-intercepts? 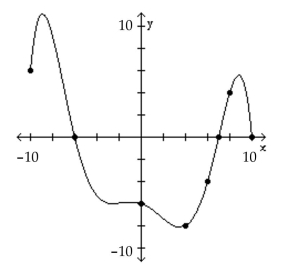
(Multiple Choice)
4.8/5  (41)
(41)
The graph of a function f is given. Use the graph to answer the question.
-For what numbers is ?
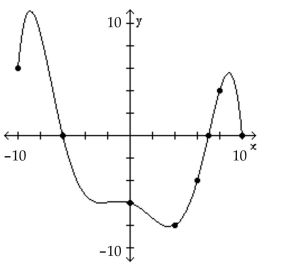
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-Express the gross salary G of a person who earns $35 per hour as a function of the number x of hours worked. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)