Exam 10: Systems of Equations and Inequalities
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one VIP ring and 2
Man-hours to make one SST ring. How many of each type of ring should be made daily to maximize the
Company's profit, if the profit on a VIP ring is $40 and on an SST ring is $35?
(Multiple Choice)
4.8/5  (44)
(44)
Graph the system of inequalities.
- + \leq36 + \geq4
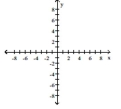 A) no solution
A) no solution
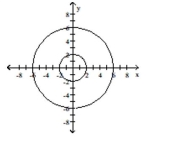 B)
B)
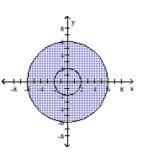 C)
C)
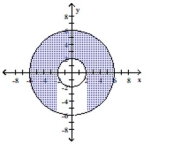 D)
D)
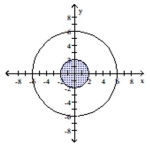
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-A doctor has told a patient to take vitamin pills. The patient needs at least 28 units of vitamin A, at least 8 units of vitamin C, and at least 76 units of vitamin D. The red vitamin pills cost 20¢ each and contain 8 units of A, 1
Unit of C, and 7 units of D. The blue vitamin pills cost 40¢ each and contain 3 units of A, 1 unit of C, and 11 units
Of D. How many pills should the patient take each day to minimize costs?
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-The liquid portion of a diet is to provide at least 300 calories, 36 units of vitamin A, and 90 units of vitamin C daily. A cup of dietary drink X provides 60 calories, 12 units of vitamin A, and 10 units of vitamin C. A cup of
Dietary drink Y provides 60 calories, 6 units of vitamin A, and 30 units of vitamin C. Set up a system of linear
Inequalities that describes the minimum daily requirements for calories and vitamins. Let x = number of cups of
Dietary drink X, and y = number of cups of dietary drink Y. Write all the constraints as a system of linear
Inequalities. A)
B)
C)
D)
(Multiple Choice)
4.8/5  (44)
(44)
Write the word or phrase that best completes each statement or answers the question.
-Find real numbers a, b, and c such that the graph of the function c contains the points (1, 1), (2, 4),
and (-3, 29).
(Short Answer)
4.8/5  (44)
(44)
Write the partial fraction decomposition of the rational expression.
-
(Multiple Choice)
4.8/5  (36)
(36)
Write the partial fraction decomposition of the rational expression.
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The difference of two numbers is 5 and the difference of their squares is 55. Find the numbers.
(Short Answer)
4.8/5  (29)
(29)
Solve the problem.
-The equation of the line passing through the distinct points and (x is given by Find the equation of the line passing through the points and .
(Multiple Choice)
4.9/5  (37)
(37)
The graph of two equations along with the points of intersection are given. Substitute the points of intersection into the
systems of equations. Are the points of intersection solutions to the system of equations (Y/N)?
-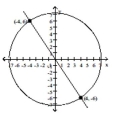 +=52 2y+3x=0
+=52 2y+3x=0
(Multiple Choice)
4.9/5  (34)
(34)
Use the properties of determinants to find the value of the second determinant, given the value of the first.
-
(Multiple Choice)
4.8/5  (29)
(29)
Showing 101 - 120 of 235
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)