Exam 10: Systems of Equations and Inequalities
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-An 8-cylinder Crown Victoria gives 18 miles per gallon in city driving and 21 miles per gallon in highway driving. A 300-mile trip required 15.5 gallons of gasoline. How many whole miles were driven in the city?
(Multiple Choice)
4.9/5  (35)
(35)
Graph the system of inequalities.
- y-x\leq5 x+y\geq3 y-3x\geq-1
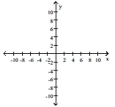 A)
A)
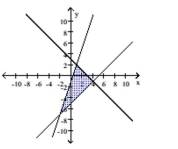 B)
B)
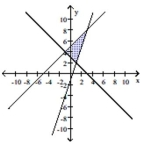 C)
C)
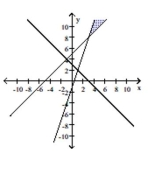 D)
D)
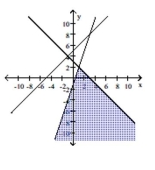
(Multiple Choice)
5.0/5  (31)
(31)
Solve the problem using matrices.
-A company manufactures three types of wooden chairs: the Kitui, the Goa, and the Santa Fe. To make a Kitui
chair requires 1 hour of cutting time, 1.5 hours of assembly time, and 1 hour of finishing time. A Goa chair
requires 1.5 hours of cutting time, 2.5 hours of assembly time and 2 hours of finishing time. A Santa Fe chair
requires 1.5 hours of cutting time, 3 hours of assembly time, and 3 hours of finishing time. If 41 hours of cutting
time, 70 hours of assembly time, and 58 hours of finishing time were used one week, how many of each type of
chair were produced?
(Short Answer)
4.9/5  (35)
(35)
Solve the problem.
-A retired couple has $170,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 5%. The rest they want to invest in AA bonds yielding 11% per year. How much
Should they invest in each to realize exactly $16,300 per year?
(Multiple Choice)
4.8/5  (38)
(38)
Write the partial fraction decomposition of the rational expression.
-
(Multiple Choice)
4.7/5  (27)
(27)
Use Cramer's rule to solve the linear system.
- A)
B)
C)
D)
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The Jillson's have up to $75,000 to invest. They decide that they want to have at least $25,000 invested in stable
bonds yielding 6% and that no more than $45,000 should be invested in more volatile bonds yielding 12%. How
much should they invest in each type of bond to maximize income if the amount in the more volatile bond
should not exceed the amount in the more stable bond? What is the maximum income?
(Short Answer)
4.8/5  (40)
(40)
Perform the indicated operation, whenever possible.
-Let and . Find
(Multiple Choice)
4.8/5  (38)
(38)
Showing 161 - 180 of 235
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)