Exam 8: Applications of Trigonometry
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Find a rectangular equation for the plane curve defined by the parametric equations.
-
(Multiple Choice)
4.9/5  (48)
(48)
Find the product. Write the product in rectangular form, using exact values.
-
(Multiple Choice)
4.9/5  (42)
(42)
Determine the number of triangles ABC possible with the given parts.
-
(Multiple Choice)
4.7/5  (41)
(41)
Find all solutions of the equation. Leave answers in trigonometric form.
-
(Multiple Choice)
4.7/5  (36)
(36)
The graph of r = aθ in polar coordinates is an example of the spiral of Archimedes. With your calculator set to radian
mode, use the given value of a and interval of θ to graph the spiral in the window specified.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A projectile is fired with an initial velocity of 450 feet per second at an angle of with the horizontal. To the nearest 10 feet, find the horizontal distance covered by the projectile.
(Multiple Choice)
4.7/5  (41)
(41)
Find all cube roots of the complex number. Leave answers in trigonometric form.
-
(Multiple Choice)
4.7/5  (31)
(31)
Solve the problem.
-A projectile is fired with an initial velocity of 600 feet per second at an angle of 45° with the horizontal. To the nearest foot, find the maximum altitude of the projectile.
(Multiple Choice)
4.7/5  (31)
(31)
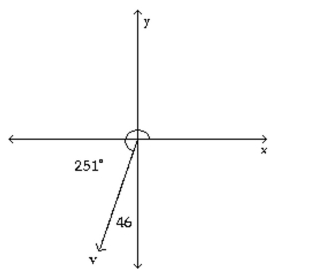
Write the vector in the form <a, b>. If necessary, round values to the nearest hundredth.
-
(Multiple Choice)
4.7/5  (39)
(39)
Solve the problem.
-Given that the polar equation models the orbits of the planets about the sun, estimate the closest possible approach of a planet for which and to a planet for which and .
(Multiple Choice)
4.8/5  (29)
(29)
Find the missing parts of the triangle.
-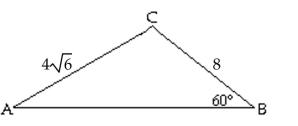 If necessary, round angles to the nearest degree and give exact values of side lengths.
If necessary, round angles to the nearest degree and give exact values of side lengths.
(Multiple Choice)
4.8/5  (38)
(38)
Draw a sketch to represent the vector. Refer to the vectors pictured here.  -
-
(Multiple Choice)
4.9/5  (30)
(30)
For the given rectangular equation, give its equivalent polar equation.
-
(Multiple Choice)
4.8/5  (38)
(38)
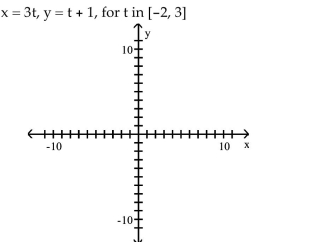
Use a table of values to graph the plane curve defined by the following parametric equations. Find a rectangular
equation for the curve.
-
(Multiple Choice)
4.7/5  (36)
(36)
Find the missing parts of the triangle.
- =9 =24 =48
If necessary, round angles to the nearest degree and give exact values of side lengths.
(Multiple Choice)
4.9/5  (36)
(36)
Find the quotient and write in rectangular form. First convert the numerator and denominator to trigonometric form.
-
(Multiple Choice)
4.9/5  (35)
(35)
Showing 281 - 300 of 446
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)