Exam 11: Further Topics in Algebra
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Solve the problem.
-A signal is made by placing 3 flags, one above the other, on a flag pole. If there are 7 different flags available, how many possible signals can be flown?
(Multiple Choice)
4.8/5  (34)
(34)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem.
-Three noncollinear points determine a triangle. How many triangles can be formed with 7 noncollinear points?
(Multiple Choice)
4.8/5  (35)
(35)
Find the first term and the common difference for the arithmetic sequence. Round approximations to the nearest
hundredth.
-
(Multiple Choice)
4.9/5  (42)
(42)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-How many different three-digit numbers can be written using digits from the set {4, 5, 6, 7, 8} without any repeating digits?
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-In how many ways can a group of 8 students be selected from 9 students?
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-In how many ways can 7 people line up for play tickets?
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-How many ways can a committee of 6 be selected from a club with 10 members?
(Multiple Choice)
4.8/5  (34)
(34)
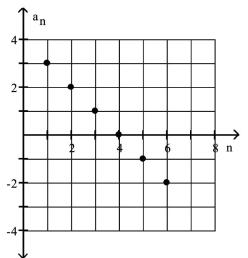
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
(Multiple Choice)
4.9/5  (40)
(40)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.7/5  (29)
(29)
Decide whether the given sequence is finite or infinite.
- for
(Multiple Choice)
5.0/5  (35)
(35)
Solve the problem.
-Suppose that an insect population density, in thousands, during year can be modeled by the recursively defined sequence: for .
Use technology to graph the sequence for . Describe what happens to the population density function.
(Multiple Choice)
4.9/5  (33)
(33)
What is the sum of the exponents on x and y in each term in a binomial expansion?
(Short Answer)
4.8/5  (34)
(34)
Decide whether the given sequence is finite or infinite.
-
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-There are 6 women running in a race. How many first, second, and third place possibilities can occur?
(Multiple Choice)
4.7/5  (42)
(42)
Showing 321 - 340 of 351
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)