Exam 11: Further Topics in Algebra

Solve the problem. -Suppose that a family has 5 children and that the probability of having a girl is $\frac { 1 } { 2 } \text {. What is the }$ probability of having exactly three girls and two boys?

Write the binomial expansion of the expression. - $( 2 m + 4 n ) ^ { 4 }$

Use the formula for S_n to find the sum of the first five terms of the geometric sequence. - $\frac { 2 } { 3 } , \frac { 4 } { 3 } , \frac { 8 } { 3 } , \frac { 16 } { 3 } , \ldots$

Evaluate the series, if it converges. - $14 + \frac { 56 } { 3 } + \frac { 224 } { 9 } + \frac { 896 } { 27 } + \ldots$

Use mathematical induction to prove that the statement is true for every positive integer n. -The series of sketches below starts with an equilateral triangle having sides of length 1 (one). In the following steps, equilateral triangles are constructed by joining the midpoints of the sides of the preceding triangle. Develop a formula for the area of the nth new triangle. Use math induction to prove your answer.

Find the first six terms of the sequence. - $a _ { 1 } = 9 , a _ { n } = a _ { n - 1 } + 7$

Solve the problem. -The beginning population of a small town was 11,000 people. Due to decline in industrial growth the population has since been decreasing at a rate of 4% every year. What was the population of This town 10 years later?

It can be shown that $( 1 + x ) ^ { n } = 1 + n x + \frac { n ( n - 1 ) } { 2 ! } x ^ { 2 } + \frac { n ( n - 1 ) ( n - 2 ) } { 3 ! } x ^ { 3 } \ldots$ is true for any real number n (not just positive integer values) and any real number x, where $| x | < 1$ Use this series to approximate the given number to the nearest thousandth. - $( 1.03 ) ^ { - 3 }$

Solve the problem. -Find the sum of the first 866 positive odd integers.

Find the common difference for the arithmetic sequence. - $2 , - 1 , - 4 , - 7 , \ldots$

Solve the problem. -A town has a population of 10,000 people and is increasing by 10% every year. What will the population be at the end of 5 years?

Write the binomial expansion of the expression. - $( a - b ) ^ { 6 }$

Find the first term and the common ratio for the geometric sequence. Round approximations to the nearest hundredth. - $a _ { 2 } = 4.5 , a _ { 7 } = 34.17$

Write the indicated term of the binomial expansion. - $( 5 x + 7 ) ^ { 3 }$ ; 3rd term

Find the nth term of the geometric sequence. - $\mathrm { a } _ { 1 } = 2 , \mathrm { r } = 5 , \mathrm { n } = 4$

Find the first term and the common ratio for the geometric sequence. Round approximations to the nearest hundredth. - $a _ { 2 } = 224 , a _ { 7 } = 7$

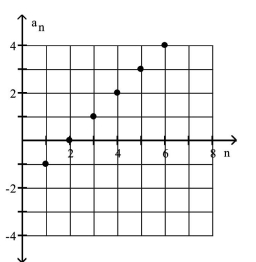
Find a formula for the nth term of the arithmetic sequence shown in the graph. -

Decide whether the given sequence is finite or infinite. - $a _ { 1 } = 2 ; \text { for } 2 \leq n \leq 15 , a _ { n } = 2 \cdot a _ { n - 1 } + 5$

Evaluate the sum using the given information. - $x _ { 1 } = - 1 , x _ { 2 } = - 4$ , and $x _ { 3 } = 0$ $\sum _ { \mathrm { i } = 1 } ^ { 3 } \left( \frac { \mathrm { x } _ { \mathrm { i } } - 3 } { 2 \mathrm { x } _ { \mathrm { i } } + 1 } \right)$

Find the sum of the first n terms of the following arithmetic sequence. - $a _ { 1 } = - 96 , d = - 8 ; \quad n = 10$