Exam 11: Further Topics in Algebra
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
List the elements in the sample space of the experiment.
-A box contains 13 white cards numbered 1 through 13. List the sample space of the event choosing one card with a number greater than 6.
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-What are the odds in favor of drawing a 1 from these cards? 
(Multiple Choice)
4.8/5  (38)
(38)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-What are the odds in favor of drawing a number greater than 2 from these cards? 
(Multiple Choice)
4.8/5  (29)
(29)
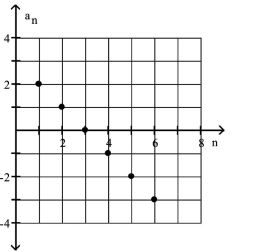
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
(Multiple Choice)
4.7/5  (31)
(31)
Provide an appropriate response.
-Consider the sequence defined by an = 41n - 98. Is this sequence arithmetic, geometric, or neither?
(Multiple Choice)
4.7/5  (47)
(47)
Solve the problem.
-A bag contains 9 apples and 7 oranges. If you select 8 pieces of fruit without looking, how many ways can you get exactly 7 apples?
(Multiple Choice)
4.7/5  (33)
(33)
Find the first term and the common difference for the arithmetic sequence. Round approximations to the nearest
hundredth.
-
(Multiple Choice)
4.8/5  (41)
(41)
It can be shown that is true for any real number n (not just positive
integer values) and any real number x, where Use this series to approximate the given number to the nearest
thousandth.
-
(Multiple Choice)
5.0/5  (38)
(38)
Find all natural number values for n for which the given statement is false.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-A die is rolled 9 times. Find the probability of rolling exactly 9 ones.
(Multiple Choice)
4.9/5  (31)
(31)
Provide an appropriate response.
-Convert the decimal to a fraction by writing it as the infinite series
(Multiple Choice)
4.7/5  (39)
(39)
Showing 101 - 120 of 351
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)