Exam 11: Further Topics in Algebra

Solve the problem. -A sequence of yearly payments of $1500 is invested at the end of every compounding period, where interest is compounded semi-annually at 1%. What is the total amount of the annuity at the End of 4 years?

Find the probability. -A lottery game contains 25 balls numbered 1 through 25. What is the probability of choosing a ball numbered 26?

Write the binomial expansion of the expression. - $\left( 3 x ^ { 2 } - y \right) ^ { 5 }$

Solve the problem. -Find the sum of all the integers from $- 47$ to 32 .

Evaluate the sum using the given information. - $x _ { 1 } = - 4 , x _ { 2 } = 5 , x _ { 3 } = 2 , x _ { 4 } = 1 , \text { and } \Delta x = - 0.8 ; f ( x ) = x ^ { 2 }$ $\sum _ { \mathrm { i } = 1 } ^ { 4 } \mathrm { f } \left( \mathrm { x } _ { \mathrm { i } } \right) \Delta \mathrm { x }$

Solve the problem. -How many ways can a committee of 2 be selected from a club with 12 members?

Solve the problem. -100 employees of a company are asked how they get to work and whether they work full time or part time. The figure below shows the results. If one of the 100 employees is randomly selected, Find the probability that the person does not work full time. 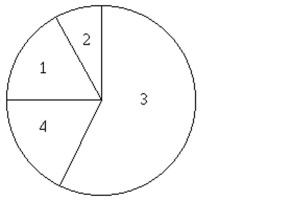1. Public transportation: 9 full time, 8 part time 2) Bicycle: 5 full time, 3 part time 3) Drive alone: 32 full time, 26 part time 4) Car pool: 7 full time, 10 part time

Use mathematical induction to prove that the statement is true for every positive integer n. - $2 ^ { n } > 2 n + 2 , \text { for } n \geq 4$

Find the probability. -A bag contains 5 red marbles, 3 blue marbles, and 1 green marble. What is the probability of choosing a marble that is not blue when one marble is drawn from the bag?

Solve the problem. -A sequence of yearly payments of $3000 is invested at an interest rate of 2%, compounded annually. What is the total amount of the annuity after 8 years?

Use mathematical induction to prove that the statement is true for every positive integer n. -The series of sketches below starts with a square having sides of length 1 (one). In the following steps, squares are constructed by joining, in order, the midpoints of the sides of the previous square. Develop a formula for the perimeter of the nth square.

Find the first term and the common difference for the arithmetic sequence. Round approximations to the nearest hundredth. - $\mathrm { S } _ { 9 } = 369$ , a $9 = 77$

Evaluate the expression. - $\frac { 10 ! } { 5 ! 5 ! }$

Evaluate the series, if it converges. - $\sum _ { i = 1 } ^ { \infty } 25 \left( \frac { 7 } { 10 } \right) ^ { i - 1 }$

Provide an appropriate response. -Consider the arrangements of sixteen students in a line. Is this a combination, a permutation, or neither?

Solve the problem. -How many ways can a president, vice-president, secretary, and treasurer be chosen from a club with 8 members? Assume that no member can hold more than one office.

It can be shown that $( 1 + x ) ^ { n } = 1 + n x + \frac { n ( n - 1 ) } { 2 ! } x ^ { 2 } + \frac { n ( n - 1 ) ( n - 2 ) } { 3 ! } x ^ { 3 } \ldots$ is true for any real number n (not just positive integer values) and any real number x, where $| x | < 1$ Use this series to approximate the given number to the nearest thousandth. - $\left( 1 - \frac { 1 } { 2 } \right) \left( 1 - \frac { 1 } { 3 } \right) \cdots \left( 1 - \frac { 1 } { n + 1 } \right) = \frac { 1 } { n + 1 }$

Graph the function corresponding to the sequence defined. Use the graph to decide whether the sequence converges or diverges. - $a _ { n } = \frac { n - 69 } { 2 n }$

Find the nth term of the geometric sequence. - $2 , - 6,18 , \ldots ; \mathrm { n } = 9$