Exam 9: Testing the Difference Between Two Means, Two Variances, and Two Proportions
Exam 1: The Nature of Probability and Statistics81 Questions
Exam 2: Frequency Distributions and Graphs107 Questions
Exam 3: Data Description127 Questions
Exam 4: Probability and Counting Rules173 Questions
Exam 5: Discrete Probability Distributions117 Questions
Exam 6: The Normal Distribution114 Questions
Exam 7: Confidence Intervals and Sample Size122 Questions
Exam 8: Hypothesis Testing178 Questions
Exam 9: Testing the Difference Between Two Means, Two Variances, and Two Proportions99 Questions
Exam 10: Correlation and Regression73 Questions
Exam 11: Other Chi-Square Tests73 Questions
Exam 12: Analysis of Variance69 Questions
Exam 13: Nonparametric Statistics62 Questions
Exam 14: Sampling and Simulation58 Questions
Select questions type
A broth used to manufacture a pharmaceutical product has its sugar content, in milligram: milliliter, measured several times on two successive days. The results are shown below.
 Can you conclude that the variability of the process is greater on the second day than on tl day? Use the level of significance. per first
Can you conclude that the variability of the process is greater on the second day than on tl day? Use the level of significance. per first
(Multiple Choice)
4.7/5  (39)
(39)
In comparing the two standard deviations below, what test value and degrees of freedom should be used in an test?
Sample 1 Sample 2 Standard deviation 7 3 Sample size 14 23
(Multiple Choice)
4.8/5  (29)
(29)
A poll found that 37% of male voters and 45% of female voters support a particular candidate. To test whether this candidate has equal levels of support between male and
Female voters, the null hypothesis should be
(Multiple Choice)
4.9/5  (43)
(43)
A study of cats and dogs found that 30 of 60 cats and 11 of 40 dogs slept more than 10 hours per day. At the 0.05 level of significance, is there sufficient evidence to conclude
That a difference exists between the proportions of cats and dogs that sleep more than 10
Hours per day?
(Multiple Choice)
4.9/5  (37)
(37)
When subjects are matched according to one variable, the matching process does not
eliminate the influence of other variables.
(True/False)
4.8/5  (37)
(37)
The critical value for a two-tailed test is when , the sample size from which the variance for the numerator was obtained is 10 , and the sample size from which the variance for the denominator was obtained is 15 .
(True/False)
4.8/5  (33)
(33)
If the test value for the difference between the means of two large samples is when the critical value is , the null hypothesis should not be rejected.
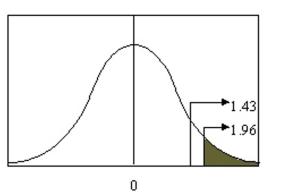
(True/False)
4.9/5  (42)
(42)
An automobile manufacturer wishes to test that claim that synthetic motor oil can improv mileage (in miles per gallon, or mpg). The table below shows the gas mileages, in mpg, o that used synthetic motor oil. The table also shows the gas mileages in mpg of six cars tha using conventional motor oil (the controls).
Synthetic: 24 28 27 28 26 26 Control: 26 25 25 27 27 27
Can you conclude that the mean gas mileage for cars using synthetic motor oil is more the the mean for the controls? Use the level of significance. as
(Multiple Choice)
4.8/5  (33)
(33)
A researcher wanted to determine if using an octane booster would increase gasoline mileage. A random sample of seven cars was selected; the cars were driven for two weeks without the booster and two weeks with the booster. Use the definitions of and as given in the table. Consequently, .
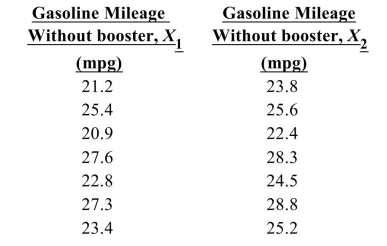 Determine the mean of the differences.
Determine the mean of the differences.
(Multiple Choice)
4.8/5  (39)
(39)
A researcher wanted to determine if using an octane booster would increase gasoline mileage. A random sample of seven cars was selected; the cars were driven for two weeks without the booster and two weeks with the booster. Use the definitions of and as given in the table. Consequently, .
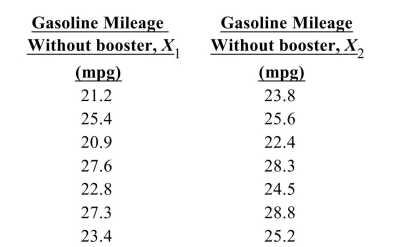 What critical value should be used at
What critical value should be used at
(Multiple Choice)
4.8/5  (45)
(45)
The average credit card debt for a recent year was . Five years earlier the average credit card debt was . Assume sample sizes of 35 were used and the population standard deviations of both samples were . Is there evidence to conclude that the average credit card debt has increased? Use .
a. State the hypotheses.
b. Find the critical value.
c. Compute the test statistic.
d. Make the decision.
e. Summarize the results.
(Essay)
4.9/5  (41)
(41)
An -test with 13 degrees of freedom in the numerator and 9 degrees of freedom in the denominator produced a test statistic whose value was . The null and alternate hypotheses were versus .
Do you reject at the level?
(Multiple Choice)
4.9/5  (33)
(33)
A researcher wanted to determine if using an octane booster would increase gasoline mileage. A random sample of seven cars was selected; the cars were driven for two weeks without the booster and two weeks with the booster. Use the definitions of and as given in the table. Consequently, .
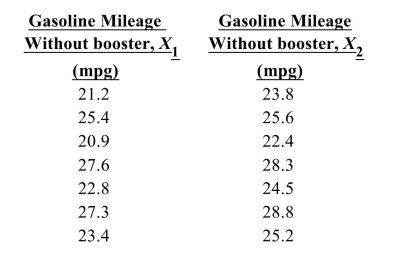 Compute the standard deviation of the differences.
Compute the standard deviation of the differences.
(Multiple Choice)
5.0/5  (42)
(42)
The concentration of hexane (a common solvent) was measured in units of micrograms per liter for a simple random sample of nineteen specimens of untreated ground water taken near a municipal landfill. The sample mean was with a sample standard deviation of 4.3. Sixteen specimens of treated ground water had an average hexane concentration of with a standard deviation of 4.7.
It is reasonable to assume that both samples come from populations that are approximatel normal. Can you conclude that the mean hexane concentration is less in treated water thar untreated water? Use the level of significance.
(Multiple Choice)
4.9/5  (36)
(36)
Following is a sample of five matched pairs.
Sample 1 20 20 23 18 22 Sample 2 23 16 15 14 18
Let and represent the population means and let . A test will be made of the hypotheses versus . Can you reject at the level of significance?
(Multiple Choice)
4.8/5  (35)
(35)
A test was made of versus . The sample means were and , the sample standard deviations were and , and the sample sizes were and .
How many degrees of freedom are there for the test statistic?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 81 - 99 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)