Exam 8: Hypothesis Testing
Exam 1: The Nature of Probability and Statistics81 Questions
Exam 2: Frequency Distributions and Graphs107 Questions
Exam 3: Data Description127 Questions
Exam 4: Probability and Counting Rules173 Questions
Exam 5: Discrete Probability Distributions117 Questions
Exam 6: The Normal Distribution114 Questions
Exam 7: Confidence Intervals and Sample Size122 Questions
Exam 8: Hypothesis Testing178 Questions
Exam 9: Testing the Difference Between Two Means, Two Variances, and Two Proportions99 Questions
Exam 10: Correlation and Regression73 Questions
Exam 11: Other Chi-Square Tests73 Questions
Exam 12: Analysis of Variance69 Questions
Exam 13: Nonparametric Statistics62 Questions
Exam 14: Sampling and Simulation58 Questions
Select questions type
Assume that a confidence interval for the mean is . The null hypothesis at would
(Multiple Choice)
4.7/5  (35)
(35)
Which type of alternative hypothesis is used in the figure below?
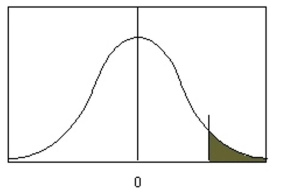
(Multiple Choice)
4.7/5  (48)
(48)
A test of versus is performed using a significance level of . The value of the test statistic is .
If the true value of is 55 , does the conclusion result in a Type I error, a Type II error, or correct decision?
(Multiple Choice)
4.9/5  (32)
(32)
Use technology to find the -value for the following values of the test statistic , sample size , and alternate hypothesis .
(Multiple Choice)
4.9/5  (32)
(32)
A test of versus is performed using a significance level of . The value of the test statistic is .
If the true value of is 59 , does the conclusion result in a Type I error, a Type II error, or correct decision?
(Multiple Choice)
4.9/5  (30)
(30)
At a water bottling facility, a technician is testing a bottle filling machine that is supposed to deliver 750 milliliters of water. The technician dispenses 43 samples of water and determines the volume of each sample. The 43 samples have a mean volume of . The machine is out of calibration if the mean volume differs from .
The technician wants to perform a hypothesis test to determine whether the machine is ou calibration. The standard deviation of the dispensed volume is known to be value of the test statistic.
(Multiple Choice)
4.8/5  (37)
(37)
A statistician claims that the standard deviation of the weights of firemen is more than 25 pounds. A sample of 20 randomly chosen firemen had a standard deviation of their weights of pounds. Assume the variable is normally distributed. At , what is the critical value for this test?
(Multiple Choice)
4.9/5  (40)
(40)
Historically, a certain region has experienced 65 thunder days annually. (A "thunder day" is day on which at least one instance of thunder is audible to a normal human ear). Over the past eleven years, the mean number of thunder days is 55 with a standard deviation of 20. Can you conclude that the mean number of thunder days is less than 65 ? Use the level of significance.
(Multiple Choice)
4.8/5  (44)
(44)
About 31% of all burglaries are through an open or unlocked door or window. A sample of 137 burglaries indicated that 88 were not via an open or unlocked door or window. At
The 0.05 level of significance, can it be concluded that this differs from the stated
Proportion?
(Multiple Choice)
4.8/5  (43)
(43)
A lumber mill is tested for consistency by measuring the variance of board thickness. The target accuracy is a variance of square inches or less. If 28 measurements are made and their variance is square inches, is there enough evidence to reject the claim that the standard deviation is within the limit at ?
(Multiple Choice)
4.8/5  (42)
(42)
The following output from MINITAB presents the results of a hypothesis test.
Test of vs. not
The assumed standard deviation 11.9
Mean SE Mean 95\% CI Z P 42 38.23 2.16239 (1.66073324,10.1373009) -1.508542 0.131416
Do you reject at the level?
(Multiple Choice)
4.7/5  (37)
(37)
A machine fills 12 -ounce bottles with soda. For the machine to function properly, the standard deviation of the sample must be less than or equal to ounce. A sample of 8 bottles is selected, and the number of ounces of soda in each bottle is given. At , can you reject the claim that the machine is functioning properly? Justify your answer. (A that the variables are approximately normally distributed.)
12.04 11.91 11.91 11.91 11.91 11.97 12.01 12.06
(Multiple Choice)
4.8/5  (31)
(31)
A test is made of versus A sample of size is drawn, and . The population standard deviation is . Compute the value of the test statistic .
(Multiple Choice)
4.9/5  (40)
(40)
The following output from MINITAB presents the results of a hypothesis test.
Test of vs. not
The assumed standard deviation
Mean SE Mean 95\% 49 54.30 2.240023 (3.36669862,12.1475871) 1.893443 0.058299
What is the value of the test statistic?
(Multiple Choice)
4.8/5  (37)
(37)
The Golden Comet is a hybrid chicken that is prized for its high egg production rate and gentle disposition. According to recent studies, the mean rate of egg production for 1-year-old Golden Comets is eggs/week.
Sarah has 40 1-year-old hens that are fed exclusively on natural scratch feed: insects, seeds, and plants that the hens obtain as they range freely around the farm. Her hens exhibit a mean egg-laying rate of eggs/day.
Sarah wants to determine whether the mean laying rate for her hens is higher than the rate for all Golden Comets. Assume the population standard deviation to be eggs/day. Compute the value of the test statistic.
(Multiple Choice)
4.9/5  (41)
(41)
A sample of 60 chewable vitamin tablets have a sample mean of 227 milligrams of vitamin C. Nutritionists want to perform a hypothesis test to determine how strong the
Evidence is that the mean mass of vitamin C per tablet exceeds 230 milligrams. State the
Appropriate null and alternate hypotheses.
(Multiple Choice)
4.8/5  (35)
(35)
Dr. Christina Cuttleman, a nutritionist, claims that the average number of calories in a serving of popcorn is 75 with a standard deviation of 7 . A sample of 50 servings of popcorn was found to have an average of 78 calories. Check Dr. Cuttleman's claim at .
(Essay)
4.8/5  (38)
(38)
Showing 101 - 120 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)