Use the following information to answer the question. Suppose the manager of a large high-end jewelry store wants to estimate the amount spent by customers during the holiday season. She took a random sample of customers and recorded the amount they spent. A histogram of the data shows that the data is strongly left-skewed. The figures below show the confidence intervals for the mean amount spent using (A) raw (untransformed) data, and (B) log-transformed data, which showed a more normally distributed data set. Use this information to answer the question. \[\begin{array}{l} \begin{array} { | l c c c c c | } \hline { \text { (A) One-Sample T: Purch } } \\ \hline \text { Variable } & \mathrm { N } & \text { Mean } & \text { StDev } & \text { SE Mean } & 95 \% \text { CI } \\ \hline \text { Purch } & 15 & 223.5 & 100.4 & 26.0 & ( 167.9,279.1 ) \\ \hline \end{array}\\\\ \begin{array} { | l c c c c c | } \hline { \text { (B) One-Sample T: LogPurch } } \\ \hline \text { Variable } & \text { N } & \text { Mean } & \text { StDev } & \text { SE Mean } & 95 \% \text { CI } \\ \hline \text { LogPurch } & 15 & 2.311 & 0.236 & 0.101 & ( 2.2,2.4 ) \\ \hline \end{array} \end{array}\] -Choose the statement that explains which confidence interval is likely to be a more precise estimate of amount spent and why.

A) The confidence interval for the geometric mean is more precise because the distribution of the log-transformed data is more symmetric. B) The confidence interval for the untransformed data is more precise because the values are in Actual dollars which is more meaningful. C) The confidence interval for the untransformed data is more precise because it is strongly Left-skewed and the confidence interval gives a wider interval. D) None of these. A) The confidence interval for the geometric mean is more precise because the distribution of the log-transformed data is more symmetric. B) The confidence interval for the untransformed data is more precise because the values are in Actual dollars which is more meaningful. C) The confidence interval for the untransformed data is more precise because it is strongly Left-skewed and the confidence interval gives a wider interval. D) None of these.

Use the following information to answer the question. Suppose the Nielson Organization conducted a survey to find out how many minutes of crime dramas that people watched in one week. Assume that all conditions for the Mann been met. Use the following test output to answer the question. Hypothesis test results: $ \mathrm{ml}= $ median for adults ages 24-39 $ \mathrm{m} 2= $ median for adults ages $ 40-55 $ Parameter: $ \mathrm{m} 1-\mathrm{m} 2 $ $\begin{array}{|l|l|l|l|l|l|l|} \hline \text { Difference } & \mathrm{n} 1 & \mathrm{n} 2 & \text { Diff.Est } & \text { Test Stat } & \text { P-value } & \text { Method } \\ \hline \mathrm{m} 1-\mathrm{m} 2 & 13 & 13 & 65 & 45.7 & 0.120 & \text { Norm. Approx. } \\ \hline \end{array}$ -State the null and alternative hypothesis to test the claim that adults between the ages of 24 and 39 and adults between the ages of 40 and 55 watch different amounts of crime dramas on television.

The answer of Use the following information to answer the...

Exam 13: Inference Without Normality

Use the following information to answer the question. Suppose the Nielson Organization conducted a survey to find out how many minutes of crime dramas that people watched in one week. Assume that all conditions for the Mann-Whitney test have been met. Use the following test output to answer the question. Hypothesis test results: $\mathrm{ml}=$ median for adults ages 24-39 $\mathrm{m} 2=$ median for adults ages $40-55$ Parameter: $\mathrm{m} 1-\mathrm{m} 2$ Difference 1 2 Diff.Est Test Stat P-value Method 1-2 13 13 65 45.7 0.120 Norm. Approx. -Using a significance level of 5%, state the correct decision regarding the null hypothesis and write a sentence which summarizes the conclusion and addresses the claim.

(Essay)

4.8/5

(42)

Question 41

You are presented with data from two independent samples. The variable being measured is continuous. The distribution of the population of each sample is right skewed. You wish to test the hypothesis that there is a difference in the median value of the variable for the samples. What type of test/method should you use? Explain why the t-test is not appropriate in this situation.

(Essay)

5.0/5

(44)

Question 42

Use the following information to answer the question. Suppose the manager of a large high-end jewelry store wants to estimate the amount spent by customers during the holiday season. She took a random sample of customers and recorded the amount they spent. A histogram of the data shows that the data is strongly left-skewed. The figures below show the confidence intervals for the mean amount spent using (A) raw (untransformed) data, and (B) log-transformed data, which showed a more normally distributed data set. Use this information to answer the question. (A) One-Sample T: Purch Variable Mean StDev SE Mean 95\% CI Purch 15 223.5 100.4 26.0 (167.9,279.1) (B) One-Sample T: LogPurch Variable N Mean StDev SE Mean 95\% CI LogPurch 15 2.311 0.236 0.101 (2.2,2.4) -Choose the statement that explains which confidence interval is likely to be a more precise estimate of amount spent and why.

(Multiple Choice)

4.8/5

(39)

Question 43

Find the mean, median, and geometric mean for the following numbers: 120, 400, 1300, and 22,000. List from smallest to largest and round to the nearest tenth.

(Multiple Choice)

4.9/5

(41)

Question 44

A new fiber bar is advertised to curb hunger for three hours. A sample of thirty-six hungry subjects were asked to record their level of hunger before eating the fiber bar and again three hours after Eating the fiber bar. Which test should be used to test the hypothesis there is no difference in the Level of hunger three hours after eating the fiber bar (i.e. the fiber bar curbed hunger for three Hours)?

(Multiple Choice)

4.8/5

(33)

Question 45

You are presented with data from two independent samples. The variable being measured is continuous. The distribution of the population of each sample is right skewed. You wish to test the Hypothesis that there is a difference in the median value of the variable for the samples. What type Test/method should you use?

(Multiple Choice)

4.9/5

(42)

Question 46

Refer to the following two histograms and QQ plots of the same data to answer the question. -For which sample might a log transform be useful? Explain. (There are no zeros or negative values in either data set.)

(Essay)

4.7/5

(32)

Question 47

Use the following information to answer the question. Can dogs lower anxiety in math class? Fifty subjects who reported anxiety about attending math class were measured for stress at the beginning of a math class then spent 15 minutes interacting with a dog followed by a forty-five minute math lecture. Each subject was then measured for stress at the end of the lecture. The hypothesis test results for the sign test are summarized below. Assume that all conditions for testing have been met: Hypothesis test results: Parameter: Median of variable : median =0 : median 0 Variable for tests Sample Median Below Equal Above P-value Difference 50 46 1 18 4 28 0.1839 -Calculate the value of the test statistic and state the value of the p-value.

(Essay)

4.7/5

(34)

Question 48

Calculate the width of both intervals (note that you will need to convert the log-transformed interval back into dollars). Which interval is narrower?

(Multiple Choice)

4.7/5

(46)

Question 49

Use the following information to answer the question. Math self-efficacy can be defined as one's belief in his or her own ability to perform mathematical tasks. A college math professor wishes to find out if her male students' math self-efficacy matches reality. To do this she gives a math quiz to the male students then asks them to rate their level of confidence in how well they did on the quiz. She plans to test whether those who had little confidence that they did well on the quiz actually performed worse than those who had a high level of confidence that they did well on the quiz. Shown below is the approximate sampling distribution of the difference in mean quiz scores. The table below shows the summary statistics for the two groups. Assume that all conditions for a randomization test have been satisfied. Group Mean Median Standard Deviation IQR High Conf. 105 82.5 84.0 7.1 12.5 Low Conf. 201 72.1 69.9 6.2 10.4 Test Stat: Mean High Conf. - Mean Low Conf. Number of simulations: 350 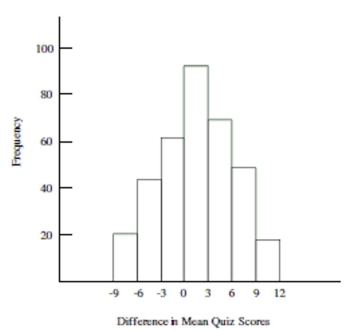$Use the following information to answer the question. Math self-efficacy can be defined as one's belief in his or her own ability to perform mathematical tasks. A college math professor wishes to find out if her male students' math self-efficacy matches reality. To do this she gives a math quiz to the male students then asks them to rate their level of confidence in how well they did on the quiz. She plans to test whether those who had little confidence that they did well on the quiz actually performed worse than those who had a high level of confidence that they did well on the quiz. Shown below is the approximate sampling distribution of the difference in mean quiz scores. The table below shows the summary statistics for the two groups. Assume that all conditions for a randomization test have been satisfied. \begin{array}{l} \begin{array} { | l | c | c | c | c | c | } \hline { \text { Group } } & \mathrm { n } & \text { Mean } & \text { Median } & \begin{array} { c } \text { Standard } \\ \text { Deviation } \end{array} & \text { IQR } \\ \hline \text { High Conf. } & 105 & 82.5 & 84.0 & 7.1 & 12.5 \\ \hline \text { Low Conf. } & 201 & 72.1 & 69.9 & 6.2 & 10.4 \\ \hline \end{array}\\ \hline \text { Test Stat: Mean High Conf. - Mean Low Conf. } \\ \hline \text { Number of simulations: } 350 \\ \end{array} -Complete the randomization test by stating the proper decision regarding the null hypothesis and the professor's conclusion. Are differences in mean quiz scores due to chance?$ -Complete the randomization test by stating the proper decision regarding the null hypothesis and the professor's conclusion. Are differences in mean quiz scores due to chance?

(Essay)

4.8/5

(39)

Question 50

Which of the following statements could be a reason to justify the use of the sign test?

(Multiple Choice)

4.9/5

(32)

Question 51

Use the following information to answer the question. Suppose the Nielson Organization conducted a survey to find out how many minutes of crime dramas that people watched in one week. Assume that all conditions for the Mann been met. Use the following test output to answer the question. Hypothesis test results: $\mathrm{ml}=$ median for adults ages 24-39 $\mathrm{m} 2=$ median for adults ages $40-55$ Parameter: $\mathrm{m} 1-\mathrm{m} 2$ Difference 1 2 Diff.Est Test Stat P-value Method 1-2 13 13 65 45.7 0.120 Norm. Approx. -State the null and alternative hypothesis to test the claim that adults between the ages of 24 and 39 and adults between the ages of 40 and 55 watch different amounts of crime dramas on television.

(Essay)

4.8/5

(36)

Question 52

Choose the correct null and alternative hypothesis to test the claim that adults between the ages of 24 and 34 and adults between the ages of 35 and 45 watch different amounts of televised sporting Events.

(Multiple Choice)

4.8/5

(29)

Question 53

Use the following information to answer the question. Suppose the Nielson Organization conducted a survey to find out how many minutes of reality-type television programming people watched in one week. Assume that all conditions for the Mann-Whitney test have been met. Use the following test output to answer the question. Hypothesis test results: $\mathrm{ml}=$ median for women $\mathrm{m} 2=$ median for men Parameter: m1-m2 Difference 1 2 Diff.Est Test Stat P-value Method 1-2 10 10 50 38.2 0.022 Norm. Approx. -Using a significance level of 5%, state the correct decision regarding the null hypothesis and the concluding statement.

(Multiple Choice)

4.7/5

(34)

Question 54

Use the following information to answer the question. Math self-efficacy can be defined as one's belief in his or her own ability to perform mathematical tasks. A college math professor wishes to find out if her female students' math self-efficacy matches reality. To do this she gives a math quiz to the female students then asks them to rate their level of confidence in how well they did on the quiz. She plans to test whether those who had little confidence that they did well on the quiz actually performed worse than those who had a high level of confidence that they did well on the quiz. Shown below is the approximate sampling distribution of the difference in mean quiz scores. The table below shows the summary statistics for the two groups. Assume that all conditions for a randomization test have been satisfied. Group Mean Median Standard Deviation IQR High Conf. 106 77.2 75.5 6.5 10.5 Low Conf. 211 62.2 59.2 5.9 9.3 Test Stat: Mean High Conf. - Mean Low Conf. Number of simulations: 350 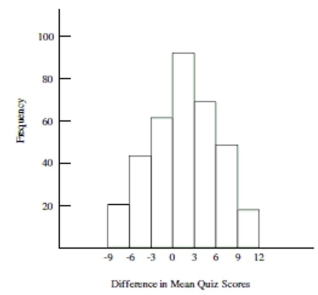$Use the following information to answer the question. Math self-efficacy can be defined as one's belief in his or her own ability to perform mathematical tasks. A college math professor wishes to find out if her female students' math self-efficacy matches reality. To do this she gives a math quiz to the female students then asks them to rate their level of confidence in how well they did on the quiz. She plans to test whether those who had little confidence that they did well on the quiz actually performed worse than those who had a high level of confidence that they did well on the quiz. Shown below is the approximate sampling distribution of the difference in mean quiz scores. The table below shows the summary statistics for the two groups. Assume that all conditions for a randomization test have been satisfied. \begin{array}{l} \begin{array} { | l | c | c | c | c | c | } \hline { \text { Group } } & \mathrm { n } & \text { Mean } & \text { Median } & \begin{array} { c } \text { Standard } \\ \text { Deviation } \end{array} & \text { IQR } \\ \hline \text { High Conf. } & 106 & 77.2 & 75.5 & 6.5 & 10.5 \\ \hline \text { Low Conf. } & 211 & 62.2 & 59.2 & 5.9 & 9.3 \\ \hline \end{array}\\\hline \text { Test Stat: Mean High Conf. } - \text { Mean Low Conf. } \\ \hline \text { Number of simulations: } 350 \\ \end{array} -Carry out the randomization test. What is the professor's conclusion? Are differences in mean quiz scores due to chance?$ -Carry out the randomization test. What is the professor's conclusion? Are differences in mean quiz scores due to chance?

(Multiple Choice)

4.9/5

(32)

Question 55

Use the following information to answer the question. Can deep-knee bends help you stay alert in class? Forty subjects were measured for alertness at the beginning of class then voluntarily performed fifteen deep-knee bends followed by a forty-five minute lecture. Each subject was then measured for alertness at the end of the lecture. The hypothesis test results for the sign test are summarized below. Assume that all conditions for testing have been met: Hypothesis test results: Parameter: Median of variable : median =0 : median 0 Variable for tests Sample Median Below Equal Above P-value Difference 40 35 1 14 5 21 0.4777 -Choose the correct null and alternative hypothesis.

(Multiple Choice)

4.8/5

(43)

Question 56

Calculate the mean, median, and geometric mean for the following numbers: 110, 500, 1700, and 31,000. List from smallest to largest and round to the nearest tenth.

(Essay)

4.9/5

(31)

Question 57

Use the following information to answer the question. Suppose the Nielson Organization conducted a survey to find out how many minutes of televised sporting events people watched in one week. Assume that all conditions for the Mann test have been met. Use the following test output to answer the question. Hypothesis test results: $\mathrm{ml}=$ median for adults ages $24-34$ $\mathrm{m} 2=$ median for adults ages $35-45$ Parameter: $\mathrm{m} 1-\mathrm{m} 2$ Difference 1 2 Diff.Est Test Stat P-value Method 1-2 12 12 65 45.7 0.120 Norm. Approx. -Using a significance level of 5%, state the correct decision regarding the null hypothesis and the concluding statement.

(Multiple Choice)

4.8/5

(45)

Question 58

Choose the statement that is not true about the Mann-Whitney Test.

(Multiple Choice)

4.7/5

(49)

Question 59

State the null and alternative hypothesis and also the value of the test statistic for the professor's randomization test.

(Multiple Choice)

4.9/5

(37)

Question 60

Showing 41 - 60 of 60

Find the mean, median, and geometric mean for the following numbers: 120, 400, 1300, and 22,000. List from smallest to largest and round to the nearest tenth.

Refer to the following two histograms and QQ plots of the same data to answer the question. -For which sample might a log transform be useful? Explain. (There are no zeros or negative values in either data set.)

Calculate the width of both intervals (note that you will need to convert the log-transformed interval back into dollars). Which interval is narrower?

Which of the following statements could be a reason to justify the use of the sign test?

Choose the correct null and alternative hypothesis to test the claim that adults between the ages of 24 and 34 and adults between the ages of 35 and 45 watch different amounts of televised sporting Events.

Calculate the mean, median, and geometric mean for the following numbers: 110, 500, 1700, and 31,000. List from smallest to largest and round to the nearest tenth.

Choose the statement that is not true about the Mann-Whitney Test.

State the null and alternative hypothesis and also the value of the test statistic for the professor's randomization test.

Introduction to Data

Picturing Variation With Graphs

Numerical Summaries of Center and Variation

Regression Analysis: Exploring Associations Between Variables

Modeling Variation With Probability

Modeling Random Events: the Normal and Binomial Models

Survey Sampling and Inference

Hypothesis Testing for Population Proportions

Inferring Population Means

Associations Between Categorical Variables

Multiple Comparisons and Analysis of Variance

Experimental Design: Controlling Variation

Inference for Regression

Filters