Exam 2: More on Functions
Exam 1: Graphs, Functions, and Models189 Questions
Exam 2: More on Functions157 Questions
Exam 3: Quadratic Functions and Equations; Inequalities209 Questions
Exam 4: Polynomial and Rational Functions94 Questions
Exam 5: Exponential and Logarithmic Functions106 Questions
Exam 6: Systems of Equations and Matrices70 Questions
Exam 7: Conic Sections59 Questions
Exam 8: Sequences, Series, and Combinatorics92 Questions
Select questions type
For the pair of functions, find the indicated sum, difference, product, or quotient.
-
Find (fg)(x)
A) (2 x+4)(5 x-4)
B)
C)
D) (2 x+4)(25 x-16)
(Short Answer)
4.8/5  (37)
(37)
For the function f, construct and simplify the difference quotient
-
(Multiple Choice)
4.9/5  (42)
(42)
Determine the domain and range of the function.
-![Determine the domain and range of the function. - A) domain: [0,4]; range: [-3,0] B) domain: [-3,0]; range: [0,4] C) domain: [0,3]; range: ( - \infty , 4 ] D) domain: ( - \infty , 4 ] range: [0,3]](https://storage.examlex.com/TB34225555/11ec84ea_9072_a9e4_9401_0334daa50438_TB34225555_11.jpg) A) domain: [0,4]; range: [-3,0]
B) domain: [-3,0]; range: [0,4]
C) domain: [0,3]; range:
D) domain: range: [0,3]
A) domain: [0,4]; range: [-3,0]
B) domain: [-3,0]; range: [0,4]
C) domain: [0,3]; range:
D) domain: range: [0,3]
(Short Answer)
4.9/5  (35)
(35)
Solve the problem.
-The intensity of light from a light source varies inversely as the square of the distance from the source. Suppose the the intensity is 40 foot-candles at a distance of 10 feet. What will the intensity be at a distance of 23 feet? Round your answer to the tenths place.
(Multiple Choice)
4.9/5  (33)
(33)
Find an equation of variation for the given situation.
-y varies directly as x and inversely as z , and y=4 when x=2 and z=6 .
(Multiple Choice)
4.9/5  (42)
(42)
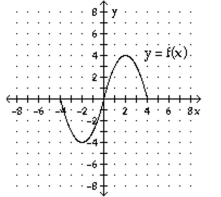
The graph of the function f is shown below. Match the function g with the correct graph.
-g(x)= f(-x)+ 4
(Multiple Choice)
4.8/5  (30)
(30)
Solve.
-A rectangular box with volume 400 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the base. Express the cost the box as a function of x.
A)
B)
C)
D)
(Short Answer)
4.8/5  (33)
(33)
For the pair of functions, find the indicated sum, difference, product, or quotient.
-
Find (f+g)(x)
(Multiple Choice)
4.9/5  (40)
(40)
Solve.
-A rectangle that is x feet wide is inscribed in a circle of radius 21 feet. Express the area of the rectangle as a function of x .
A) 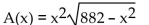 B)
B) 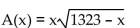 C)
C) 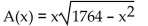 D)
D) 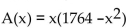
(Short Answer)
4.9/5  (32)
(32)
Find an equation of variation for the given situation.
-y aries jointy as x and p and inverely as the square of s, and when x=1, p=1, and s=2 .
A)
B)
C)
D)
(Short Answer)
4.8/5  (39)
(39)
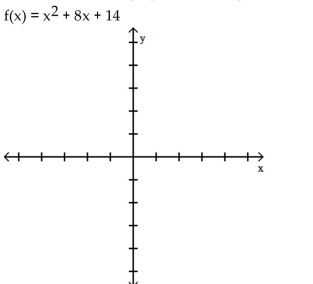
Graph the function. Use the graph to find any relative maxima or minima.
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The force needed to keep a car from skidding on a curve varies jointly as the weight of the car and the square of the car's speed, and inversely as the radius of the curve. If a force of 3600 pounds is needed to keep an 1800 pound car traveling at 20 mph from skidding on a curve of radius 600 feet, What force would be required to keep the same car from skidding on a curve of radius 700 feet at 30 mph? Round your answer to the nearest pound of force?
(Multiple Choice)
4.8/5  (27)
(27)
Answer the question.
-How can the graph of 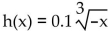 be obtained from the graph of
be obtained from the graph of 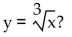 A) Reflect it across the y-axis. Stretch it vertically by a factor of 1 .
B) Reflect it across the x -axis. Stretch it vertically by a factor of 1 .
C) Reflect it across the x-axis. Shrink it vertically by a factor of 0.1 .
D) Reflect it across the y-axis. Shrink it vertically by a factor of 0.1 .
A) Reflect it across the y-axis. Stretch it vertically by a factor of 1 .
B) Reflect it across the x -axis. Stretch it vertically by a factor of 1 .
C) Reflect it across the x-axis. Shrink it vertically by a factor of 0.1 .
D) Reflect it across the y-axis. Shrink it vertically by a factor of 0.1 .
(Short Answer)
4.8/5  (31)
(31)
For the pair of functions, find the indicated sum, difference, product, or quotient.
-f(x)=x+5, g(x)=x-4
Find (f+g)(-4) .
(Multiple Choice)
4.8/5  (41)
(41)
Solve.
-A rectangular box with volume 517 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent
The length of a side of the base in feet. Express the cost of the box as a function of x and then graph
This function. From the graph find the value of x, to the nearest hundredth of a foot, which will
Minimize the cost of the box.
(Multiple Choice)
4.9/5  (42)
(42)
For the pair of functions, find the indicated domain.
-
Find the domain of
A)
B)
C) (-6,6)
D)
(Short Answer)
4.9/5  (28)
(28)
Showing 61 - 80 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)