Exam 2: More on Functions
Exam 1: Graphs, Functions, and Models189 Questions
Exam 2: More on Functions157 Questions
Exam 3: Quadratic Functions and Equations; Inequalities209 Questions
Exam 4: Polynomial and Rational Functions94 Questions
Exam 5: Exponential and Logarithmic Functions106 Questions
Exam 6: Systems of Equations and Matrices70 Questions
Exam 7: Conic Sections59 Questions
Exam 8: Sequences, Series, and Combinatorics92 Questions
Select questions type
Solve.
-Elissa wants to set up a rectangular dog run in her backyard. She has 36 feet of fencing to work with and wants to use it all. If the dog run is to be x feet long, express the area of the dog run as a
Function of x.
A)
B)
C)
D)
(Short Answer)
4.8/5  (38)
(38)
A graph of y = f(x) follows. No formula for f is given. Graph the given equation.
-
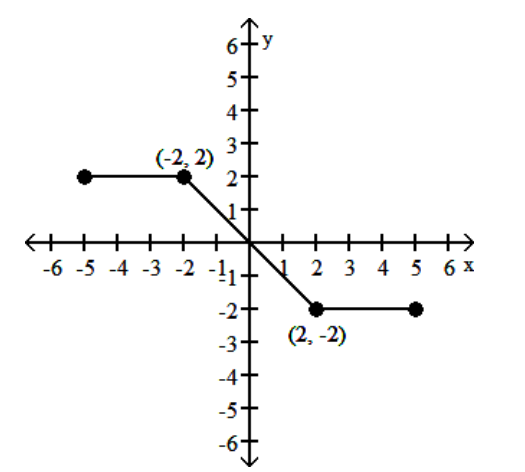
(Multiple Choice)
5.0/5  (36)
(36)
Find an equation of variation for the given situation.
- y varies inversely as x and y=0.1 when x=0.5
(Multiple Choice)
4.8/5  (45)
(45)
Find the point that is symmetric to the given point with respect to the requested axis.
-Symmetric with respect to the y-axis (1.5,1.75)
A) (1.5,-1.5)
B) (1.75,1.5)
C) (-1.5,-1.75)
D) (-1.5,1.75)
(Short Answer)
4.7/5  (39)
(39)
Solve.
-Sue wants to put a rectangular garden on her property using 66 meters of fencing. There is a river that runs through her property so she decides to increase the size of the garden by using the river as One side of the rectangle. (Fencing is then needed only on the other three sides.)Let x represent the length of the side of the rectangle along the river. Express the garden's area as a function of x.
(Multiple Choice)
4.8/5  (36)
(36)
Find an equation of variation for the given situation.
- y varies inversely as x and y=6 when
A)
в)
C)
D)
(Short Answer)
4.8/5  (41)
(41)
Consider the functions F and G as shown in the graph. Provide an appropriate response.
-Find the domain of G/F.
![Consider the functions F and G as shown in the graph. Provide an appropriate response. -Find the domain of G/F. A) [ - 1,2 ) \cup ( 2,3 ) B) (-1,3] C) [-3,4] D) [-3,3]](https://storage.examlex.com/TB34225555/11ec84ea_d34c_c4d7_9401_d5fd606f4d2f_TB34225555_11.jpg) A)
B) (-1,3]
C) [-3,4]
D) [-3,3]
A)
B) (-1,3]
C) [-3,4]
D) [-3,3]
(Short Answer)
4.8/5  (28)
(28)
Consider the functions F and G as shown in the graph. Provide an appropriate response.
-Find the domain of F + G.
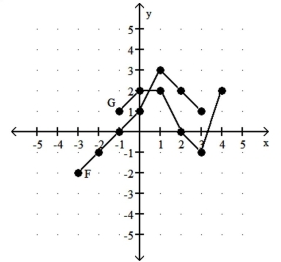
(Multiple Choice)
4.9/5  (41)
(41)
For the piecewise function, find the specified function value.
-
F(-7)
(Multiple Choice)
5.0/5  (43)
(43)
Find an equation of variation for the given situation.
- y varies jointly as x and z and inversely as the product of w and p , and when x=1, z=6 , w=20 and p=8 .
(Multiple Choice)
4.9/5  (38)
(38)
Find the point that is symmetric to the given point with respect to the requested axis.
-Symmetric with respect to the x -axis (7,2)
(Multiple Choice)
4.8/5  (40)
(40)
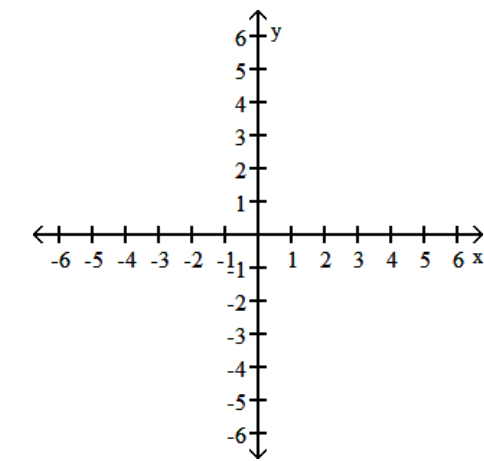
A graph of y = f(x) follows. No formula for f is given. Graph the given equation.
-y = 2f(x)
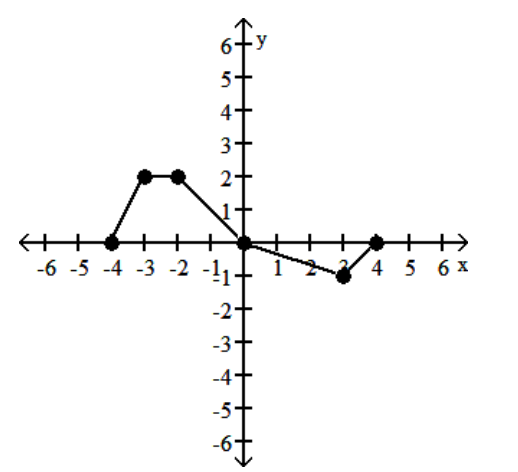
(Multiple Choice)
4.7/5  (33)
(33)
Determine algebraically whether the graph is symmetric with respect to the x-axis, the y-axis, and the origin.
-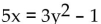
(Multiple Choice)
4.9/5  (45)
(45)
Write an equation for a function that has a graph with the given characteristics.
-The shape of y=|x| is vertically stretched by a factor of 6.2 . This graph is then reflected across the x -axis. Finally, the graph is shifted 0.15 units downward.
(Multiple Choice)
4.8/5  (47)
(47)
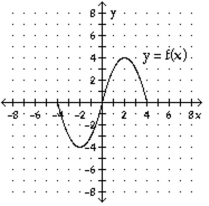
The graph of the function f is shown below. Match the function g with the correct graph.
-g(x)= f(x)-4
(Multiple Choice)
4.9/5  (33)
(33)
Showing 81 - 100 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)