Exam 3: Systems of Linear Equations
Exam 1: Algebra, Mathematical Models, and Problem Solving181 Questions
Exam 2: Functions and Linear Functions138 Questions
Exam 3: Systems of Linear Equations104 Questions
Exam 4: Inequalities and Problem Solving100 Questions
Exam 5: Polynomials, Polynomial Functions, and Factoring127 Questions
Exam 6: Rational Expressions, Functions, and Equations102 Questions
Exam 7: Radicals, Radical Functions, and Rational Exponents98 Questions
Exam 8: Quadratic Equations and Functions115 Questions
Select questions type
Solve the problem.
-A company's expenses included many factors. In 2012, travel costs were 2.97% of the expense budget , increasing by 0.21% of the total expense budget per year. In 2012, office supplies were 5.80% of the expense budget, increasing by 0.03% of the total expense budget per year. In which year will the cost of travel expenses and office supplies be the same? For that year, what will be the cost of each expense as a percentage of the total expense budget?
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-One number is 3 less than a second number. Twice the second number is 2 less than 4 times the first. Find the two numbers.
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 10 feet more than 2 times the width. He needs 68 feet of fencing to do the job. Find the length and width of the garden.
(Multiple Choice)
4.7/5  (40)
(40)
Solve the system. If there is no solution or if the system's equations are dependent, so state.
-
(Multiple Choice)
4.9/5  (30)
(30)
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 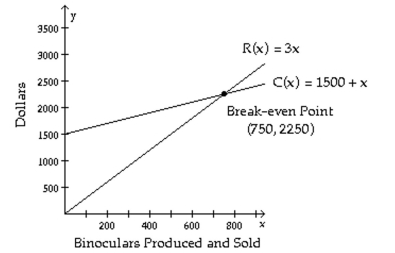 -At the break-even point both cost and revenue are what?
-At the break-even point both cost and revenue are what?
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Julie and Eric row their boat (at a constant speed) 24 miles downstream for 4 hours, helped by the current. Rowing at the same rate, the trip back against the current takes 6 hours. Find the rate of the current.
(Multiple Choice)
4.8/5  (27)
(27)
Solve the system. If there is no solution or if the system's equations are dependent, so state.
-
(Multiple Choice)
4.9/5  (41)
(41)
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question.  -Use the revenue and cost functions to write the profit function from producing and selling x binoculars.
-Use the revenue and cost functions to write the profit function from producing and selling x binoculars.
(Multiple Choice)
4.7/5  (26)
(26)
Solve the problem.
-Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product. C(x)=6000x+24,000 R(x)=8000x
(Multiple Choice)
4.9/5  (37)
(37)
Determine if the given ordered triple is a solution of the system.
-
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the system is inconsistent, dependent, or neither.
-
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-A vendor sells hot dogs, bags of potato chips, and soft drinks. A customer buys 5 hot dogs, 5 bags of potato chips, and 2 soft drinks for $11.50. The price of a hot dog is $1.00 more than the price of a bag of potato chips. The cost of a soft drink is $2.25 less than the price of two hot dogs. Find the cost of each item.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
C(x)=1.7x+700 R(x)=2.7x
(Multiple Choice)
4.7/5  (33)
(33)
Showing 41 - 60 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)