Exam 2: Functions and Linear Functions
Exam 1: Algebra, Mathematical Models, and Problem Solving181 Questions
Exam 2: Functions and Linear Functions138 Questions
Exam 3: Systems of Linear Equations104 Questions
Exam 4: Inequalities and Problem Solving100 Questions
Exam 5: Polynomials, Polynomial Functions, and Factoring127 Questions
Exam 6: Rational Expressions, Functions, and Equations102 Questions
Exam 7: Radicals, Radical Functions, and Rational Exponents98 Questions
Exam 8: Quadratic Equations and Functions115 Questions
Select questions type
Find the slope of the line that goes through the given points.
-
(Multiple Choice)
4.9/5  (41)
(41)
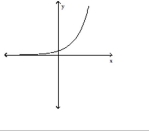
Use the vertical line test to determine whether or not the graph is a graph of a function.
-
(Multiple Choice)
4.8/5  (37)
(37)
Rewrite the given equation in slope-intercept form by solving for y.
--2x + 7y = 0 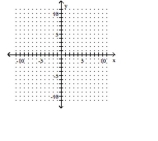
(Multiple Choice)
4.9/5  (32)
(32)
Decide whether the relation is a function.
-{(3, 6), (3, 4), (5, -2), (7, -5), (11, 6)}
(Multiple Choice)
4.9/5  (26)
(26)
Find the slope of the line that goes through the given points.
-
(Multiple Choice)
4.8/5  (31)
(31)
Find the domain and range.
-{(6,-6), (-4,7), (9,8), (9,-1)}
(Multiple Choice)
4.8/5  (38)
(38)
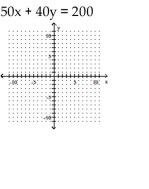
Use intercepts and a checkpoint to graph the linear function.
-
(Multiple Choice)
4.8/5  (37)
(37)
Rewrite the given equation in slope-intercept form by solving for y.
-
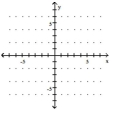
(Multiple Choice)
4.9/5  (44)
(44)
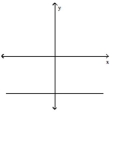
Use the vertical line test to determine whether or not the graph is a graph of a function.
-
(Multiple Choice)
4.9/5  (38)
(38)
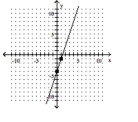
Find the slope of the line that goes through the given points.
-
(Multiple Choice)
4.9/5  (27)
(27)
For the pair of functions, determine the domain of f + g.
-
(Multiple Choice)
4.7/5  (30)
(30)
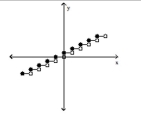
Use the vertical line test to determine whether or not the graph is a graph of a function.
-
(Multiple Choice)
4.8/5  (29)
(29)
For the pair of functions, determine the domain of f + g.
-
(Multiple Choice)
4.7/5  (38)
(38)
Use the graph to find the indicated function value.
-y = f(x). Find f(4). 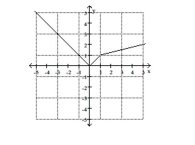
(Multiple Choice)
4.9/5  (23)
(23)
Showing 61 - 80 of 138
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)