Exam 3: Functions
Exam 1: Equations, Inequalities, and Applications221 Questions
Exam 2: The Rectangular Coordinate System, Lines, and Circles140 Questions
Exam 3: Functions247 Questions
Exam 4: Polynomial and Rational Functions255 Questions
Exam 5: Exponential and Logarithmic Functions and Equations186 Questions
Exam 6: Conic Sections97 Questions
Exam 7: Systems of Equations and Inequalities226 Questions
Exam 8: Matrices83 Questions
Exam 9: Sequences and Series; Counting and Probability255 Questions
Exam 10: Math Exercises: Sets, Intervals, Absolute Value, and Properties298 Questions
Select questions type
Graph the function by starting with the graph of the basic function and then using the techniques of shifting, compressing, stretching, and/or reflecting.
-
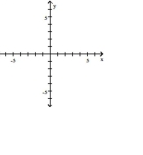
(Multiple Choice)
4.8/5  (43)
(43)
Find the x-intercept(s)and the y-intercept of the function.
-f(x)= -2
(Multiple Choice)
4.7/5  (40)
(40)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting, compressing, stretching, and/or reflecting.
-
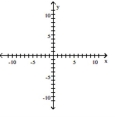
(Multiple Choice)
4.8/5  (45)
(45)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given interval.
-(- 1, 0) 
(Multiple Choice)
4.7/5  (39)
(39)
For the given functions f and g, find the requested function and state its domain. Write the domain in interval notation.
- Find
(Multiple Choice)
4.8/5  (29)
(29)
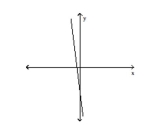
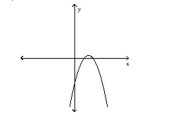
Use the vertical line test to determine whether the graph represents a function.
-
(Multiple Choice)
4.9/5  (43)
(43)
Find the domain of the composite function f g. Write the domain in interval notation.
-
(Multiple Choice)
4.7/5  (36)
(36)
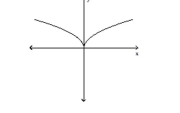
Use the horizontal line test to determine whether the function is one-to-one.
-
(Multiple Choice)
5.0/5  (32)
(32)
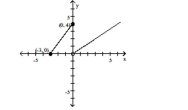
Find the rule that defines each piecewise-defined function.
-
(Multiple Choice)
4.9/5  (41)
(41)
Use the vertical line test to determine whether the graph represents a function.
-
(Multiple Choice)
4.8/5  (33)
(33)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given interval.
-Find the values of x, if any, at which f has a relative maximum. What are the relative maxima? 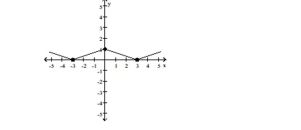
(Multiple Choice)
4.8/5  (42)
(42)
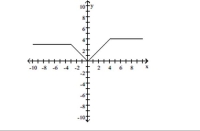
Use the graph to determine the function's domain and range. Write the domain and range in interval notation.
-
(Multiple Choice)
4.8/5  (33)
(33)
For the given functions f and g, find the requested composite function.
- Find the function .
(Multiple Choice)
4.7/5  (34)
(34)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting, compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (37)
(37)
Decide whether or not the functions are inverses of each other.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A cellular phone plan had the following schedule of charges: 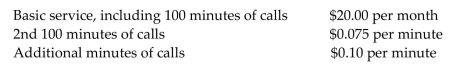 What is the charge for 200 minutes of calls in one month? What is the charge for 250 minutes of calls in one month? Construct a function that relates the monthly charge C for x minutes of calls.
What is the charge for 200 minutes of calls in one month? What is the charge for 250 minutes of calls in one month? Construct a function that relates the monthly charge C for x minutes of calls.
(Essay)
4.8/5  (46)
(46)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting, compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (42)
(42)
The graph of a function f is given. Use the graph to answer the question.
-Find the values of x, if any, at which f has a relative minimum. What are the relative minima? 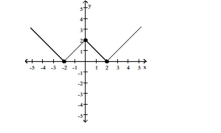
(Multiple Choice)
5.0/5  (36)
(36)
Use the accompanying graph of y = f(x) to sketch the graph of the indicated equation.
-

(Multiple Choice)
4.9/5  (45)
(45)
Showing 221 - 240 of 247
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)