Chat with AIExam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
Knowing that FN represents the Nth Fibonacci number, and given that F20 = 6765 and F21 = 10946 , find F24 .
Free
(Short Answer)
4.8/5 
(37)
(37) Correct Answer:
Verified
Verified46368
If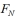 
represents the 
Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule , 
. Which of the following equations is not valid?
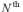represents the Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule ,
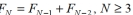. Which of the following equations is not valid?Free
(Multiple Choice)
4.8/5 (35)
(35) Correct Answer:Verified
VerifiedE
Use Binet's formula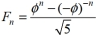 
, where 
is the golden ratio, to find the forty-third Fibonacci number 
.
, where 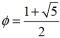is the golden ratio, to find the forty-third Fibonacci number 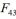.Free
(Multiple Choice)
4.9/5 (44)
(44) Correct Answer:Verified
VerifiedD
If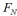 
represents the 
Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule 
- Which of the following equations is valid?
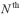represents the Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule
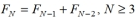- Which of the following equations is valid? (Multiple Choice)
4.9/5 (31)
(31) Find the value x so that the shaded figure is a gnomon to the white triangle.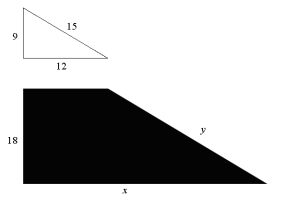 
(Short Answer)
4.9/5 (24)
(24) Use Binet's formula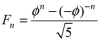 
,where 
is the golden ratio, to find the forty third Fibonacci number 
.
,where 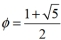is the golden ratio, to find the forty third Fibonacci number 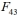. (Short Answer)
4.8/5 (36)
(36) 
=4181 and 
=10946 , find 
. Suppose that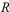 
and 
are two similar rectangles where the width of 
is 3 a and the width of 
is 5 a . If the perimeter of 
is 42 inches, then what is the perimeter of 
in inches?
and 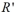are two similar rectangles where the width of 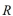is 3 a and the width of 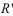is 5 a . If the perimeter of 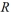is 42 inches, then what is the perimeter of 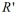in inches? (Multiple Choice)
4.8/5 (43)
(43) Rectangle A has dimensions of 3 by 6. Rectangle B is a gnomon to rectangle A. What are the
dimensions of rectangle B?
(Short Answer)
4.9/5 (39)
(39) Find the value x so that the shaded figure is a gnomon to the white triangle.
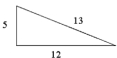
(Multiple Choice)
4.8/5 (29)
(29) Suppose that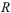 
and 
are two similar rectangles where the width of 
is 3a and the width of 
is 7a . If the perimeter of 
is 18 inches, then what is the perimeter of 
in inches?
and 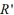are two similar rectangles where the width of 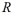is 3a and the width of 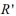is 7a . If the perimeter of 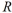is 18 inches, then what is the perimeter of 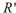in inches? (Multiple Choice)
4.8/5 (28)
(28) Find the product of the first six numbers in the Fibonacci sequence.
(Short Answer)
4.7/5 (34)
(34) 
A painter is constructing a rectangular canvas for her next masterpiece. She plans to construct the canvas so that the ratio of the larger side to the smaller side is equivalent to the golden ratio. If the smaller side is 416 \mathrm{~cm} in length, then what is the length of the larger side in centimeters? Round the answer to the nearest whole number.
(Multiple Choice)
4.8/5 (44)
(44) The golden ratio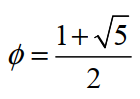 
is an irrational number. Explain what it means for a number to be irrational.
is an irrational number. Explain what it means for a number to be irrational. (Essay)
4.9/5 (37)
(37) Find the value y so that the shaded figure is a gnomon to the white triangle.
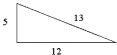
(a) 24
(b) 26
(c) 36
(d) 42
(e) None of the above.
(a) 24
(b) 26
(c) 36
(d) 42
(e) None of the above. (Short Answer)
4.9/5 (33)
(33) If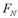 
represents the 
Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule 
. Is the following rule correct? Explain.
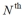represents the Fibonacci number, then the Fibonacci sequence can be constructed by the recursive rule
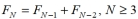. Is the following rule correct? Explain.
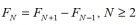
(Essay)
5.0/5 (28)
(28) Rectangle A has dimensions of 2 by 8. Rectangle B is a gnomon to rectangle
A. What are the dimensions of rectangle B?
(Short Answer)
4.7/5 (35)
(35) Find the sum of the first six numbers in the Fibonacci sequence.
(Short Answer)
4.9/5 (25)
(25) Suppose that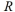 
and 
are two similar rectangles where the width of 
is a and the width of 
is 4a . If the area of 
is 64 square inches, then what is the area of 
in square inches?
and 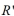are two similar rectangles where the width of 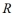is a and the width of 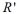is 4a . If the area of 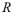is 64 square inches, then what is the area of 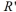in square inches? (Short Answer)
4.8/5 (44)
(44) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)