Exam 1: The Mathematics of Elections: the Paradoxes of Democracy
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
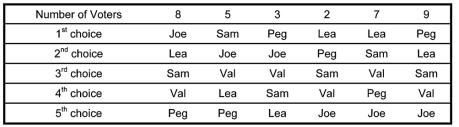 -According to the preference schedule from problem 1, which candidate, if any, will receive a majority
of 5th choice votes?
-According to the preference schedule from problem 1, which candidate, if any, will receive a majority
of 5th choice votes?
Free
(Short Answer)
4.8/5  (40)
(40)
Correct Answer:
Joe
 -According to the preference schedule from problem 1, Sam would be voted the next Campus Idol using the Plurality Method. Would this result be a violation of the Condorcet Criterion? Explain.
-According to the preference schedule from problem 1, Sam would be voted the next Campus Idol using the Plurality Method. Would this result be a violation of the Condorcet Criterion? Explain.
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
Yes, because Frank is the Condorcet
candidate and thus should be the
winner.
 -According to the preference schedule from problem 1, rank the five students using the Plurality Method.
-According to the preference schedule from problem 1, rank the five students using the Plurality Method.
Free
(Essay)
4.9/5  (32)
(32)
Correct Answer:
Peg 1st, Lea 2nd, Joe 3rd, Sam 4th, Val
5th
 -According to the preference schedule from problem 1, who is the winner of the election using the Plurality Method?
-According to the preference schedule from problem 1, who is the winner of the election using the Plurality Method?
(Multiple Choice)
4.9/5  (35)
(35)
 -Which Fairness Criterion is being violated by the actions shown in problems 7 and 8?
-Which Fairness Criterion is being violated by the actions shown in problems 7 and 8?
(Essay)
4.9/5  (30)
(30)
Five students are taking part in the Campus Talent Show. Each of the five students will perform their talent in front of an audience and once all the performers have finished the audience members will rank each participant in order of preference. The candidate who has the highest ranking will move on to the national competition. The final preference schedule is given below.
 Rank the five students using the Borda Count Method.
Rank the five students using the Borda Count Method.
(Essay)
4.9/5  (34)
(34)
An election with four candidates (A, B, C, and D) and 180 voters will use the Plurality Method to choose a winner. After 120 ballots have been recorded, A has 26 1st choice votes, B has 18 1st choice votes, C has 42 1st choice votes, and D has 34 1st choice votes. What is the minimum number of the remaining 60 1st choice votes that A must receive in order to guarantee that no candidate will receive a majority of 1st choice votes?
(Multiple Choice)
4.7/5  (36)
(36)
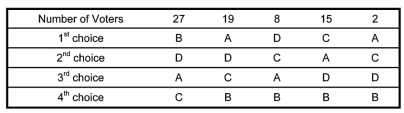 -Using the preference schedule from problem 1 , who is the winner of the election using the Method of Pairwise Comparisons?
-Using the preference schedule from problem 1 , who is the winner of the election using the Method of Pairwise Comparisons?
(Multiple Choice)
4.7/5  (32)
(32)
Using the Borda Count Method, rank the contestants from the following election.
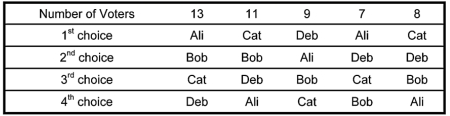
(Multiple Choice)
4.8/5  (29)
(29)
 -Using the preference schedule from problem 1 , who is the winner of the election using the Plurality with Elimination Method?
-Using the preference schedule from problem 1 , who is the winner of the election using the Plurality with Elimination Method?
(Multiple Choice)
4.9/5  (22)
(22)
The Plurality with Elimination method can possibly violate which of the Fairness Criteria?
(Multiple Choice)
4.9/5  (30)
(30)
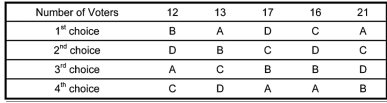
An election consists of four candidates A , B , C , D . The candidates are ranked in order of preference by each of the voters. The preference schedule for this election is given below.
 Which candidate, if any, received a majority of 1st choice votes?
Which candidate, if any, received a majority of 1st choice votes?
(Multiple Choice)
4.9/5  (39)
(39)
Since 2011, a total of 68 college basketball teams quality for the NCAA March Madness Tournament. These teams play each other in a series of games in a bracket style competition resulting in a total of 67 games. However, suppose that each team was required to play one game against everyone other participating team in a round-robin style tournament. How many games would this entail?
(Short Answer)
5.0/5  (32)
(32)
 -According to the preference schedule from problem 1, who would be the next Campus Idol if the Borda Count Method was used to choose the winner?
-According to the preference schedule from problem 1, who would be the next Campus Idol if the Borda Count Method was used to choose the winner?
(Short Answer)
4.8/5  (41)
(41)
 -According to the preference schedule from problem 1, who is the winner of the election using the Method of Pairwise Comparisons?
-According to the preference schedule from problem 1, who is the winner of the election using the Method of Pairwise Comparisons?
(Multiple Choice)
4.7/5  (24)
(24)
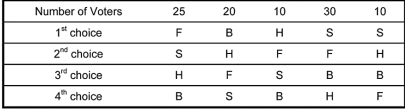
Your college radio station is holding auditions to find the next Campus Idol. There are four people competing in the auditions: Beth (B), Frank (F), Helen (H), and Sam (S). After all of the competitors have auditioned, the audience members rank each contestant in order of preference and submit their ballots. The results are given below.
 How many preference ballots were cast in this competition?
How many preference ballots were cast in this competition?
(Short Answer)
4.9/5  (35)
(35)
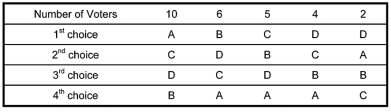
 -According to the preference schedule from problem 9 , if Cat drops out of the race and all votes shift up one slot, then who will win the race using the Borda Count Method?
-According to the preference schedule from problem 9 , if Cat drops out of the race and all votes shift up one slot, then who will win the race using the Borda Count Method?
(Multiple Choice)
4.9/5  (41)
(41)
The Student Government at your college consists of 184 voting members. A motion regarding funding
for a new club activity is brought to the floor. The four possible activities for which a member could
vote are the Karaoke Club (K), Hiking Club (H), Jousting Club (J) and Dog-Lovers Club (D). If the
Karaoke Club (K) receives a total of 48 votes, then what is the minimum number of votes needed by
one of the remaining clubs to ensure that no club can receive a majority of all votes?
(Short Answer)
4.7/5  (19)
(19)
Which of the four Voting Methods (Plurality, Borda Count, Plurality with Elimination or Pairwise Comparison) will never violate the Majority Criterion and the Condorcet Criterion?
(Short Answer)
4.9/5  (38)
(38)
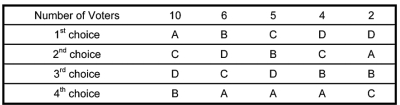 -Use the scenario and preference schedule from problem 7. Suppose that Dana is asked to be president of the Latin Club and has to withdraw from the race before the results are made public. Realign the preference table by removing D and shifting all of the votes up one slot. Now who would be chosen as the president of the Math Club using the Plurality with Elimination Method?
-Use the scenario and preference schedule from problem 7. Suppose that Dana is asked to be president of the Latin Club and has to withdraw from the race before the results are made public. Realign the preference table by removing D and shifting all of the votes up one slot. Now who would be chosen as the president of the Math Club using the Plurality with Elimination Method?
(Short Answer)
4.9/5  (35)
(35)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)