Exam 6: The Mathematics of Touring: Traveling Salesman Problems
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
For the weighted graph shown below, find the optimal tour and write your answer using A as the starting and ending vertex. 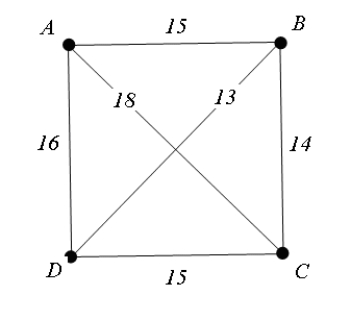
Free
(Short Answer)
4.8/5  (34)
(34)
Correct Answer:
A, B, C, D, A or A, D, C, B, A
How many edges are there in the complete graph K12 ?
Free
(Short Answer)
4.8/5  (31)
(31)
Correct Answer:
66
Consider the graph shown below; how many Hamilton Paths are there from vertex A to vertex F ?
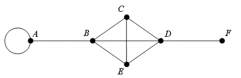
Free
(Multiple Choice)
5.0/5  (34)
(34)
Correct Answer:
C
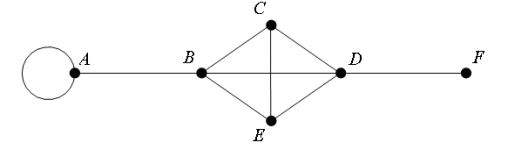 -Consider the graph above ; how many Hamilton Paths are there starting at vertex A and ending at vertex F?
-Consider the graph above ; how many Hamilton Paths are there starting at vertex A and ending at vertex F?
(Short Answer)
4.9/5  (40)
(40)
Suppose that in solving a TSP (traveling salesman problem) you use the cheapest-link algorithm and find that the length of the tour is 15,000 miles. If the optimal tour has a length of 12,000 miles, then what is the relative error of your cheapest-link tour? Express your answer as a percentage.
(Short Answer)
4.8/5  (42)
(42)
The game Doodle-Chip consists of moving a marker around a board. Once on a square, the marker can move to any other square which is adjacent (shares a side) with the square occupied. Is it possible to
Place the marker on the board at position A, move to every other square once and only once, and end
On square labeled B?
(Multiple Choice)
4.9/5  (33)
(33)
For the graph shown below, how many distinct Hamilton Paths start at A and end at F? 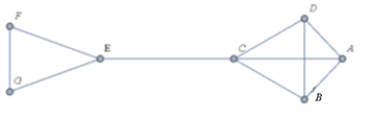
(Short Answer)
4.9/5  (37)
(37)
For the weighted graph shown below, apply the cheapest-link algorithm and find the cost of the resulting tour. 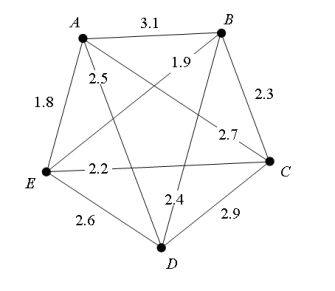
(Short Answer)
4.8/5  (39)
(39)
For the weighted graph below, apply the repetitive nearest-neighbor algorithm and give its cost. 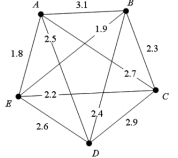
(Multiple Choice)
4.9/5  (42)
(42)
Consider the graph shown below; how many Hamilton Paths are there from vertex A to vertex F ?
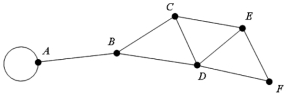
(Multiple Choice)
4.8/5  (33)
(33)
The chart below shows the one-way charge for a taxi-ride between five different cities. Give the cost of the tour found by applying the cheapest-link algorithm. 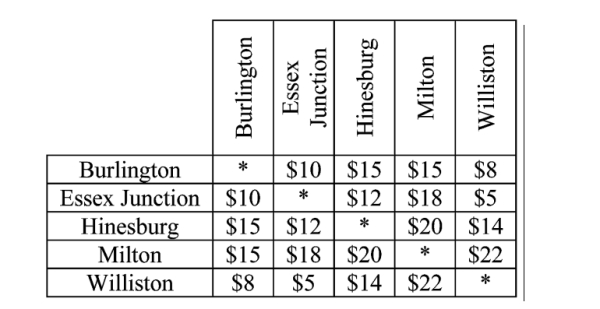
(Short Answer)
4.9/5  (45)
(45)
How many distinct Hamilton Circuits, if any, are there in the graph shown below? (Mirror images of a circuit are considered distinct or different from the circuit.) 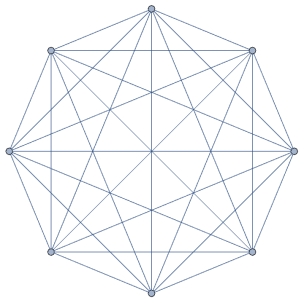
(Short Answer)
4.7/5  (35)
(35)
For the graph shown below, find a Hamilton Circuit using vertex A as your starting and ending point. 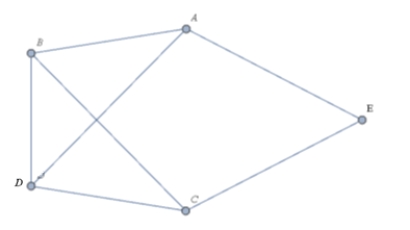
(Essay)
4.9/5  (32)
(32)
Draw a graph which has a Hamilton Circuit but does not have an Euler Circuit.
(Essay)
4.7/5  (34)
(34)
Consider the weighted graph given below; apply the nearest-neighbor algorithm with vertex F as a starting vertex and give the resulting tour.
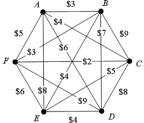
(Multiple Choice)
4.8/5  (39)
(39)
For the weighted graph below, apply the repetitive nearest-neighbor algorithm and write the resulting tour using vertex D as a starting and ending vertex. 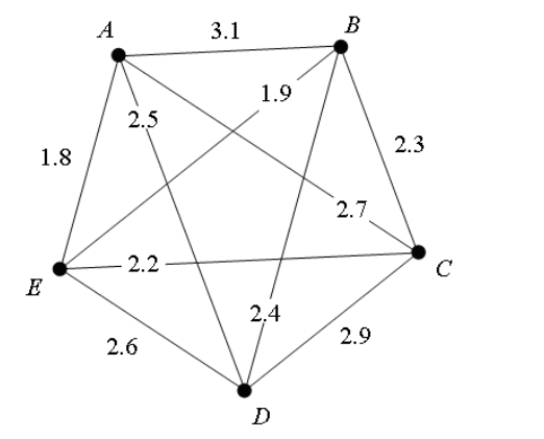
(Short Answer)
4.7/5  (39)
(39)
The game Doodle-Chip consists of moving a marker around a board. Once on a square, the marker can move to any other square which is diagonal (kitty-corner) with the square occupied. Is it possible to place the marker on the board at position A, move to every other square once and only once, and end
on the square labeled B?
(a) Yes
(b) No 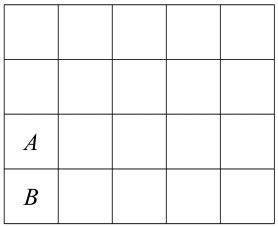
(Short Answer)
4.9/5  (38)
(38)
For the weighted graph shown below, apply the nearest-neighbor algorithm with C as a starting vertex and find the cost of the resulting tour. 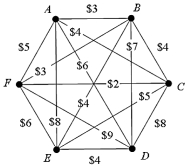
(Short Answer)
4.8/5  (39)
(39)
The chart below shows the average travel time in minutes between five different cities. Give the total time (cost) of the tour found by applying the cheapest-link algorithm. 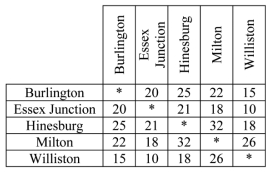
(Multiple Choice)
4.8/5  (45)
(45)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)