Exam 17: The Mathematics of Normality: the Call of the Bell
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
The graph below is of a normal curve. The shaded portion of the graph represents 68% of the total area under the curve. According to the graph, what is the value of the 97.5th percentile P97.5 ?
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
E
An honest six-sided die is tossed a total of n = 324 times and the number of times that the die lands on an even number (2, 4, or 6) is recorded. What is the probability that between 162 and 171 of the tosses Result in an even number? Give your answer as a percentage.
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
The graph below is of a normal curve. The shaded portion of the graph represents 95 % of the total area under the curve. According to the graph, what is the value of the 84th percentile P84 ?
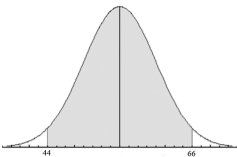
Free
(Short Answer)
4.9/5  (33)
(33)
Correct Answer:
60.5
In a normal distribution with a standard deviation of 8, the number 83 has a standardized value of 2.5.
What is the mean of this normal distribution?
(Short Answer)
4.7/5  (33)
(33)
A normal distribution has a mean of 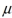 and a standard deviation of
and a standard deviation of 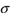 . Suppose that you know that 2.5th percentile P25=8 and the 84th percentile P84=29 . Find the mean of this normal distribution.
. Suppose that you know that 2.5th percentile P25=8 and the 84th percentile P84=29 . Find the mean of this normal distribution.
(Multiple Choice)
4.8/5  (33)
(33)
After finishing college, you start working as a quality control agent at a local manufacturing plant. The machine that you are in charge of produces steel bolts. Your job is to fine tune the machine so that it produces a specific size bolt, but a small margin of error is allowable. Suppose that you believe that the machine has been calibrated so that the actual size of a bolt produced has an approximate normal
distribution with a mean of 25 cm and a standard deviation of 0.001 cm. After producing 1000 bolts,
you randomly choose one and find that it measures 24.9995 cm. Based off of this measurement, do you think that the machine has been properly calibrated? Explain.
(Essay)
4.9/5  (34)
(34)
An honest six-sided die is tossed a total of n = 324 times and the number of times that the die lands on an even number (2, 4, or 6) is recorded. What is the probability that between 144 and 171 of the tosses Result in an even number? Give your answer as a percentage.
(Multiple Choice)
4.9/5  (32)
(32)
The actual weight of the contents of an 11-ounce bag of potato chips has an approximate normal
distribution with a mean of 11.6-ounces and a standard deviation of 0.2-ounces. What is the
probability of randomly picking a bag with an actual weight greater than 11.8-ounces? Give your
answer as a percentage.
(Short Answer)
4.8/5  (31)
(31)
The height of an 18-year old student at your university has an approximate normal distribution with a mean of 68 inches and a standard deviation of 2.5 inches. What is the first quartile of height in this Distribution? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
After several weeks of compiling data you determine that 36% of emails that you receive are spam-
emails while the remaining 64% are not. Suppose that you receive 625 emails in a week, what is the
probability that between 201 and 225 of the emails are spam-emails? Give your answer as a
percentage.
(Short Answer)
5.0/5  (41)
(41)
In a normal distribution with a standard deviation of 8 , the number 25 has a standardized value of -2.5 . What is the 84th percentile P84 of this normal distribution?
(Multiple Choice)
4.9/5  (35)
(35)
An honest coin is tossed a total of n = 1600 times and the number of heads obtained is recorded. What
is the probability that the coin lands heads greater than 840 times? Give your answer as a percentage.
(Short Answer)
4.9/5  (34)
(34)
In a normal distribution with a mean of 18, the number 25 has a standardized value of 1.6. What is the standard deviation of this normal distribution?
(Short Answer)
4.8/5  (31)
(31)
After several weeks of compiling data you determine that 36% of emails that you receive are spam-
emails while the remaining 64% are not. Suppose that you receive 2500 emails in a week, what is the
probability that less than 876 of the emails are spam-emails? Give your answer as a percentage.
(Short Answer)
4.8/5  (34)
(34)
A normal distribution has a mean of 80 and a standard deviation of 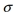 . If the 2.5th percentile is P2.5=72 , then find the standard deviation
. If the 2.5th percentile is P2.5=72 , then find the standard deviation 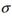 .
.
(Short Answer)
4.8/5  (40)
(40)
A normal distribution has a mean of 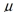 and a standard deviation of
and a standard deviation of 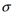 . Suppose that you know that 16th percentile P16=23 and the 97.5th percentile P97.5=62 . Find the mean of this normal distribution.
. Suppose that you know that 16th percentile P16=23 and the 97.5th percentile P97.5=62 . Find the mean of this normal distribution.
(Multiple Choice)
4.8/5  (34)
(34)
The graph below is of a normal curve. The shaded portion of the graph represents 68 % of the total area under the curve. According to the graph, what is the value of the 99.85th percentile P99.85 ?
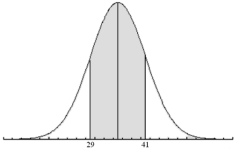
(Multiple Choice)
4.8/5  (32)
(32)
The time that it takes an Olympic runner to finish the 100-meter dash is approximately normal with a mean of 9.83 seconds with a standard deviation of 0.06 seconds. What is the probability it would take The runner less than 10.01 seconds to finish the race? Give your answer as a percentage.
(Multiple Choice)
4.8/5  (30)
(30)
The height of an 18-year old student at your university has an approximate normal distribution with a mean of 68 inches and a standard deviation of 2.5 inches. What is the third quartile of height in this Distribution? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (46)
(46)
The time that it takes an Olympic runner to finish the 100-meter dash is approximately normal with a mean of 9.83 seconds with a standard deviation of 0.06 seconds. What is the probability it would take The runner more than 9.89 seconds to finish the race? Give your answer as a percentage.
(Multiple Choice)
4.8/5  (28)
(28)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)