Exam 7: Conic Sections
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Use the center, vertices, and asymptotes to graph the hyperbola.
-
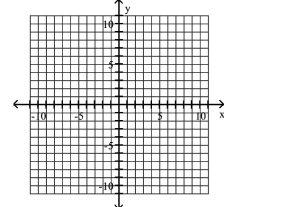
(Multiple Choice)
4.7/5  (39)
(39)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate
system and finding points of intersection.
-
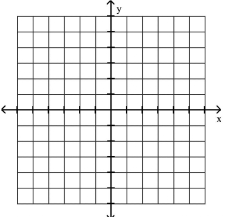
(Multiple Choice)
5.0/5  (39)
(39)
Convert the equation to the standard form for a hyperbola by completing the square on x and y.
-
(Multiple Choice)
4.8/5  (39)
(39)
Graph Hyperbolas Centered at the Origin
Use vertices and asymptotes to graph the hyperbola. Find the equations of the asymptotes.
-
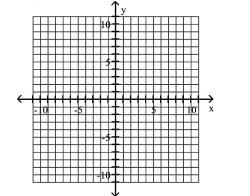
(Multiple Choice)
4.8/5  (43)
(43)
Additional Concepts
Use the relation's graph to determine its domain and range.
-
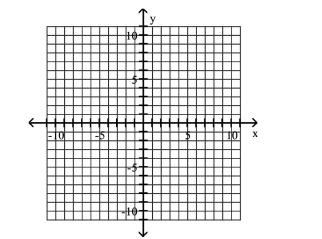
(Multiple Choice)
4.9/5  (34)
(34)
Graph Parabolas with Vertices Not at the Origin
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.8/5  (32)
(32)
Additional Concepts
Use the relation's graph to determine its domain and range.
-
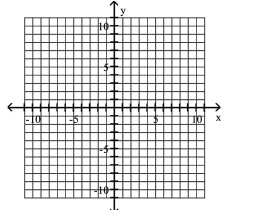
(Multiple Choice)
4.9/5  (40)
(40)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (42)
(42)
Graph Parabolas with Vertices Not at the Origin
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the vertex and the direction in which the parabola opens to determine the relation's domain and range.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Foci: ; vertices:
(Multiple Choice)
4.7/5  (35)
(35)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)