Exam 7: Conic Sections
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Convert the equation to the standard form for a parabola by completing the square on x or y as appropriate.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate
system and finding points of intersection.
- x=(y+10-1 (x-10+(y+10=1
(Multiple Choice)
4.7/5  (44)
(44)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Foci: -intercepts: and 5
(Multiple Choice)
4.9/5  (40)
(40)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.7/5  (43)
(43)
Graph Hyperbolas Centered at the Origin
Use vertices and asymptotes to graph the hyperbola. Find the equations of the asymptotes.
-
(Multiple Choice)
4.8/5  (29)
(29)
Use the center, vertices, and asymptotes to graph the hyperbola.
-
(Multiple Choice)
4.9/5  (37)
(37)
Graph Parabolas with Vertices Not at the Origin
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.8/5  (34)
(34)
Graph Parabolas with Vertices Not at the Origin
Find the vertex, focus, and directrix of the parabola with the given equation.
-
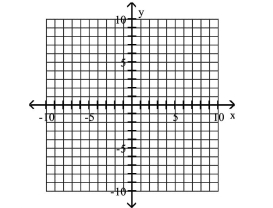
(Multiple Choice)
4.8/5  (33)
(33)
Find the vertices and locate the foci for the hyperbola whose equation is given.
-
(Multiple Choice)
4.8/5  (29)
(29)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Major axis vertical with length 14; length of minor axis = 6; center (0, 0)
(Multiple Choice)
4.8/5  (26)
(26)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Major axis horizontal with length 20; length of minor axis = 16; center (0, 0)
(Multiple Choice)
4.9/5  (32)
(32)
Additional Concepts
Use the relation's graph to determine its domain and range.
-
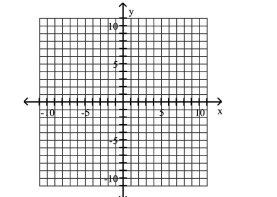
(Multiple Choice)
4.8/5  (39)
(39)
Write Equations of Hyperbolas in Standard Form
-Foci: (0, -5), (0, 5); vertices: (0, -3), (0, 3)
(Multiple Choice)
4.8/5  (35)
(35)
Solve Applied Problems Involving Hyperbolas
Solve the problem.
-Two recording devices are set 2600 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 400 feet from point B, a small amount of explosive is detonated. The recording devices record the time the sound reaches each one. How far directly north of site B should a second explosion be done so that the measured time difference recorded by the devices is the same as that for the first detonation?
(Multiple Choice)
4.8/5  (34)
(34)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.7/5  (36)
(36)
Convert the equation to the standard form for a hyperbola by completing the square on x and y.
-
(Multiple Choice)
4.9/5  (33)
(33)
Write Equations of Hyperbolas in Standard Form
-Endpoints of transverse axis: ; foci:
(Multiple Choice)
4.8/5  (39)
(39)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)