Exam 7: Conic Sections
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Write Equations of Hyperbolas in Standard Form
-Endpoints of transverse axis: ; asymptote:
(Multiple Choice)
4.8/5  (39)
(39)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find the standard form of the equation of the ellipse satisfying the given conditions.
-Foci: -intercepts: and 5
(Multiple Choice)
4.8/5  (37)
(37)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate
system and finding points of intersection.
-
(Multiple Choice)
4.8/5  (40)
(40)
Write Equations of Parabolas in Standard Form
Find the standard form of the equation of the parabola using the information given.
-Vertex: ; Focus:
(Multiple Choice)
4.8/5  (41)
(41)
Graph Hyperbolas Centered at the Origin
Use vertices and asymptotes to graph the hyperbola. Find the equations of the asymptotes.
-
(Multiple Choice)
4.8/5  (49)
(49)
Find the vertices and locate the foci for the hyperbola whose equation is given.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A reflecting telescope has a parabolic mirror for which the distance from the vertex to the focus is 25 feet. If the distance across the top of the mirror is 58 inches, how deep is the mirror in the center?
(Multiple Choice)
4.8/5  (40)
(40)
Use the vertex and the direction in which the parabola opens to determine the relation's domain and range.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve Applied Problems Involving Hyperbolas
Solve the problem.
-A satellite following the hyperbolic path shown in the picture turns rapidly at and then moves closer and closer to the line as it gets farther from the tracking station at the origin. Find the equation that describes the path of the satellite if the center of the hyperbola is at .
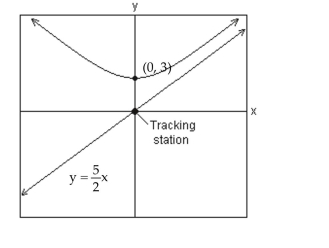
(Multiple Choice)
4.8/5  (37)
(37)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (39)
(39)
Graph Parabolas with Vertices at the Origin
Find the focus and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 170 feet and a maximum height of 30 feet. Find the height of the arch at 15 feet from its center.
(Multiple Choice)
4.8/5  (39)
(39)
Use the center, vertices, and asymptotes to graph the hyperbola.
-
(Multiple Choice)
4.8/5  (39)
(39)
Graph Hyperbolas Not Centered at the Origin
Find the location of the center, vertices, and foci for the hyperbola described by the equation.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve Applied Problems Involving Ellipses
Solve the problem.
-The arch beneath a bridge is semi-elliptical, a one-way roadway passes under the arch. The width of the roadway is 30 feet and the height of the arch over the center of the roadway is 13 feet. Two trucks plan to
Use this road. They are both 10 feet wide. Truck 1 has an overall height of 12 feet and Truck 2 has an
Overall height of 13 feet. Draw a rough sketch of the situation and determine which of the trucks can pass
Under the bridge.
(Multiple Choice)
4.8/5  (42)
(42)
Find the solution set for the system by graphing both of the system's equations in the same rectangular coordinate
system and finding points of intersection.
-
(Multiple Choice)
4.9/5  (31)
(31)
Graph Hyperbolas Centered at the Origin
Use vertices and asymptotes to graph the hyperbola. Find the equations of the asymptotes.
-
(Multiple Choice)
4.8/5  (37)
(37)
Showing 41 - 60 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)