Exam 5: Systems of Equations and Inequalities

Solve the problem. -The Jillson's have up to $75,000 to invest. They decide that they want to have at least $40,000 invested in stable bonds yielding 6% and that no more than $20,000 should be invested in more volatile bonds yielding 12%. (a)Using x to denote the amount of money invested in the stable bonds and y the amount invested in the more volatile bonds, write a system of linear inequalities that describe the possible amounts of each investment. (b)Graph the system of inequalities.

Graph the solution set of the system of inequalities or indicate that the system has no solution. - x+4y\geq-4 x>-4 y\leq6

Decompose P/Q, Where Q Has Repeated Linear Factors Write the form of the partial fraction decomposition of the rational expression. It is not necessary to solve for the constants. - $\frac { x + 4 } { x ^ { 3 } - 2 x ^ { 2 } + x }$

Solve the system by the method of your choice. Identify systems with no solution and systems with infinitely many solutions, using set notation to express their solution sets. - 2x+y=7 4x+2y=14

Graph the inequality. -y + 4 < x

Solve the system by the substitution method. - x-2y=3 -xy=20

Graph the solution set of the system of inequalities or indicate that the system has no solution. - y\geq2x-4 x+2y\leq7 x\geq-2 y\leq1

Solve the problem. -A steel company produces two types of machine dies, part A and part B. The company makes a $2.00 profit on each part A that it produces and a $6.00 profit on each part B that it produces. Let x = the number Of part A produced in a week and y = the number of part B produced in a week. Write the objective Function that describes the total weekly profit.

Determine if the given ordered triple is a solution of the system. - (3,5,1) x-y+z=-1 x+y+z=9 x+y-z=7

Solve the system by the method of your choice. Identify systems with no solution and systems with infinitely many solutions, using set notation to express their solution sets. - y=10-4x 16x+4y=40

Solve the problem. -One number is 6 less than a second number. Twice the second number is 27 more than 3 times the first. Find the two numbers.

Determine if the given ordered triple is a solution of the system. - (1,-3,3) 2x+4y+z=-5 4x-3y-z=20 4x+y+3z=12

Solve the problem. -A basketball player scored 33 points in a game. The number of three-point field goals the player made was 7 less than three times the number of free throws (each worth 1 point). Twice the number of two-point Field goals the player made was 9 more than the number of three-point field goals made. Find the number Of free-throws, two-point field goals, and three-point field goals that the player made in the game.

Solve the system by the substitution method. - y=-13 +=25

Solve the problem. -In the town of Milton Lake, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing. Let x represent the number of years since 1990 and y represent the percentage of women in Milton Lake Who smoke. The graph of y against x includes the data points (0, 16.6)and (13, 19.98). Let x represent the Number of years since 1990 and y represent the percentage of men in Milton Lake who smoke. The graph Of y against x includes the data points (0, 28.8)and (14, 25.86). Determine when the percentage of women who smoke will be the same as the percentage of men who Smoke. Round to the nearest year. What percentage of women and what percentage of men (to the nearest Whole percent)will smoke at that time? [Hint: first find the slope-intercept equation of the line that models the percentage, y, of women who Smoke x years after 1990 and the slope-intercept equation of the line that models the percentage, y, of men Who smoke x years after 1990]

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 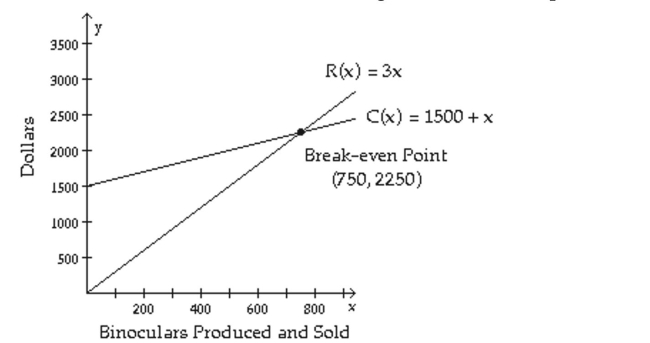-Is there a profit when 323 binoculars are produced?

Graph the solution set of the system of inequalities or indicate that the system has no solution. - $1 \leq y<10$

Graph the inequality. - $y \leq 2^{x}$

Solve the problem. -Joely's Tea Shop, a store that specializes in tea blends, has available 45 pounds of A grade tea and 70 pounds of B grade tea. These will be blended into 1 pound packages as follows: A breakfast blend that contains one third of a pound of A grade tea and two thirds of a pound of B grade tea and an afternoon tea that contains one half pound of A grade tea and one half pound of B grade tea. If Joely makes a profit of $1.50 on each pound of the breakfast blend and $2.00 profit on each pound of the afternoon blend, how many pounds of each blend should she make to maximize profits? What is the maximum profit?

Solve the problem. -An-Mei owns a business making and selling jackets. She has a fixed cost of $4050. It costs $69 to produce each jacket. The selling price is $96 per jacket. Let x represent the number of jackets produced and sold And write the cost function, C, and revenue function, R.