Question 1

Solve the system of equations by the substitution method.
-$$\begin{aligned}
y & = 5 x + 4 \
5 y - 15 x & = 30
\end{aligned}$$

Accepted Answer

A)  $\{ ( 1,9 ) \}$ 
B)  $\{ ( 9,1 ) \}$ 
C)  $\{ ( - 1,9 ) \}$ 
D)  $\varnothing$ 
A)  $\{ ( 1,9 ) \}$ 
B)  $\{ ( 9,1 ) \}$ 
C)  $\{ ( - 1,9 ) \}$ 
D)  $\varnothing$

Question 2

Solve the problem.
-A right triangle has an area of 44 square inches. The square of the hypotenuse is 185. Find the lengths of the legs of the triangle. Round your answer to the nearest inch.

Accepted Answer

A) 8 inches and 11 inches 
B) 64 inches and 121 inches 
C) 4 inches and 22 inches 
D) 16 inches and 5.5 inches 
A) 8 inches and 11 inches 
B) 64 inches and 121 inches 
C) 4 inches and 22 inches 
D) 16 inches and 5.5 inches

Question 3

Graph the solution set of the system of inequalities or indicate that the system has no solution.
-$\begin{array}{l}
y<x+1 \
9 x+10 y>30
\end{array}$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 4

Solve the problem.
-A vineyard produces two special wines, a white and a red. A bottle of the white wine requires 14 pounds of grapes and 1 hour of processing time. A bottle of red wine requires 25 pounds of grapes and 2 hours of
Processing time. The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing
Time to the production of these wines. A bottle of the white wine sells for $11.00, while a bottle of the red
Wine sells for $20.00. How many bottles of each type should the vineyard produce in order to maximize
Gross sales?

Accepted Answer

A) 132 bottles of white and 14 bottles of red 
B) 14 bottles of white and 132 bottles of red 
C) 76 bottles of white and 42 bottles of red 
D) 42 bottles of white and 59 bottles of red 
A) 132 bottles of white and 14 bottles of red 
B) 14 bottles of white and 132 bottles of red 
C) 76 bottles of white and 42 bottles of red 
D) 42 bottles of white and 59 bottles of red

Question 5

Solve the problem.
-The liquid portion of a diet is to provide at least 300 calories, 36 units of vitamin A, and 90 units of vitamin C daily. A cup of dietary drink X provides 60 calories, 12 units of vitamin A, and 10 units of vitamin C. A
Cup of dietary drink Y provides 60 calories, 6 units of vitamin A, and 30 units of vitamin C. Set up a system
Of linear inequalities that describes the minimum daily requirements for calories and vitamins. Let x =
Number of cups of dietary drink X, and y = number of cups of dietary drink Y. Write all the constraints as
A system of linear inequalities.

Accepted Answer

A) $\begin{array}{l}
60 x+60 y \geq 300 \
12 x+6 y \geq 36 \
10 x+30 y \geq 90 \
x \geq 0 \
y \geq 0
\end{array}$ 
B) $ \begin{array}{l}
60 x+60 y>300 \
12 x+6 y>36 \
10 x+30 y>90 \
x>0 \
y>0
\end{array}$ 
C) $\begin{array}{l}
60 x+60 y \geq 300 \
12 x+6 y>36 \
10 x+30 y \geq 90
\end{array}$ 
D) $\begin{array}{l}
60 x+60 y \leq 300 \
12 x+6 y \leq 36 \
10 x+30 y \leq 90 \
x \geq 0 \
y \geq 0
\end{array}$ 
A) $\begin{array}{l}
60 x+60 y \geq 300 \
12 x+6 y \geq 36 \
10 x+30 y \geq 90 \
x \geq 0 \
y \geq 0
\end{array}$ 
B) $ \begin{array}{l}
60 x+60 y>300 \
12 x+6 y>36 \
10 x+30 y>90 \
x>0 \
y>0
\end{array}$ 
C) $\begin{array}{l}
60 x+60 y \geq 300 \
12 x+6 y>36 \
10 x+30 y \geq 90
\end{array}$ 
D) $\begin{array}{l}
60 x+60 y \leq 300 \
12 x+6 y \leq 36 \
10 x+30 y \leq 90 \
x \geq 0 \
y \geq 0
\end{array}$

Question 6

Solve Nonlinear Systems By Addition
Solve the system by the addition method.
-$$\begin{array} { l } 
6 x ^ { 2 } + y ^ { 2 } = 36 \
6 x ^ { 2 } - y ^ { 2 } = 36
\end{array}$$

Accepted Answer

A)  $\{ ( \sqrt { 6 } , 0 ) , ( - \sqrt { 6 } , 0 ) \}$ 
B)  $\{ ( 6,0 ) , ( - 6,0 ) \}$ 
C)  $\{ ( 0 , \sqrt { 6 } ) , ( 0 , - \sqrt { 6 } ) \}$ 
D)  $\{ ( 0,6 ) , ( 0 , - 6 ) \}$ 
A)  $\{ ( \sqrt { 6 } , 0 ) , ( - \sqrt { 6 } , 0 ) \}$ 
B)  $\{ ( 6,0 ) , ( - 6,0 ) \}$ 
C)  $\{ ( 0 , \sqrt { 6 } ) , ( 0 , - \sqrt { 6 } ) \}$ 
D)  $\{ ( 0,6 ) , ( 0 , - 6 ) \}$

Question 7

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells
binoculars. Use the information in the figure to answer the question.
  
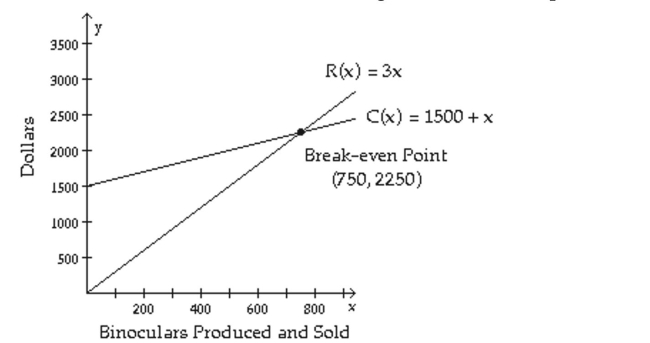-Use the revenue and cost functions to write the profit function from producing and selling x binoculars.

Accepted Answer

A) P(x)= 2x - 1500 
B) P(x)= 2x + 1500 
C) P(x)= 4x + 1500 
D) P(x)= 4x - 1500 
A) P(x)= 2x - 1500 
B) P(x)= 2x + 1500 
C) P(x)= 4x + 1500 
D) P(x)= 4x - 1500

Question 8

Solve the system by the substitution method.
-$x ^ { 2 } = y ^ { 2 } + 39$ $x - y = 3$

Accepted Answer

A)  $\{ ( 8,5 ) \}$ 
B)  $\{ ( 8 , - 5 ) \}$ 
C)  $\{ ( - 8,5 ) \}$ 
D)  $\{ ( - 8 , - 5 ) \}$ 
A)  $\{ ( 8,5 ) \}$ 
B)  $\{ ( 8 , - 5 ) \}$ 
C)  $\{ ( - 8,5 ) \}$ 
D)  $\{ ( - 8 , - 5 ) \}$

Question 9

Solve the problem.
-In 1985, in the town of Appleby, 22.8% of Hispanics were overweight, increasing by an average of 0.47% per year. In 1985, in the town of Appleby, 0.17% of whites were overweight, increasing by an average of
29.2% per year. Write a function that models the percentage, y, of Hispanics who are overweight x years
After 1985. Write a function that models the percentage, y, of whites who are overweight x years after 1985.

Accepted Answer

A)  Hispanics: $y = 0.47 x + 22.8$
Whites: $\mathrm { y } = 29.2 \mathrm { x } + 0.17$ 
B)  Hispanics: $y = 22.8 x + 0.47$
Whites: $y = 0.17 x + 29.2$ 
C)  Hispanics: $y = 23.27 x$
Whites: $\mathrm { y } = 29.37 \mathrm { x }$ 
D)  Hispanics: $y + 0.47 x = 22.8$
Whites: $\mathrm { y } + 29.2 \mathrm { x } = 0.17$ 
A)  Hispanics: $y = 0.47 x + 22.8$
Whites: $\mathrm { y } = 29.2 \mathrm { x } + 0.17$ 
B)  Hispanics: $y = 22.8 x + 0.47$
Whites: $y = 0.17 x + 29.2$ 
C)  Hispanics: $y = 23.27 x$
Whites: $\mathrm { y } = 29.37 \mathrm { x }$ 
D)  Hispanics: $y + 0.47 x = 22.8$
Whites: $\mathrm { y } + 29.2 \mathrm { x } = 0.17$

Question 10

Solve the problem.
-A dietitian needs to purchase food for patients. She can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. Let x = the number of ounces of chicken and y = the number of ounces of
Potatoes purchased per patient. Write the objective function that describes the total cost per patient per
Meal.

Accepted Answer

A)  $z = 0.25 x + 0.02 y$ 
B)  $z = 0.02 x + 0.25 y$ 
C)  $z = 25 x + 2 y$ 
D)  $z = 2 y + 25 y$ 
A)  $z = 0.25 x + 0.02 y$ 
B)  $z = 0.02 x + 0.25 y$ 
C)  $z = 25 x + 2 y$ 
D)  $z = 2 y + 25 y$

Question 11

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells
binoculars. Use the information in the figure to answer the question.
  
-Is there a profit when 947 binoculars are produced?

Accepted Answer

A) Yes 
B) No 
A) Yes 
B) No

Question 12

Graph the inequality.
-$$( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9$$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 13

Solve the system of equations by the substitution method.
-$$\begin{array} { l } 
5 x - 6 y = 2 - 5 x \
2 x + 6 y = x + 5 y + - 3
\end{array}$$

Accepted Answer

A)  $\{ ( - 1 , - 2 ) \}$ 
B)  $\{ ( - 1,2 ) \}$ 
C)  $\{ ( 0,2 ) \}$ 
D)  $\left\{ \left[ \frac { 1 } { 5 } , 0 \right\} \right\}$ 
A)  $\{ ( - 1 , - 2 ) \}$ 
B)  $\{ ( - 1,2 ) \}$ 
C)  $\{ ( 0,2 ) \}$ 
D)  $\left\{ \left[ \frac { 1 } { 5 } , 0 \right\} \right\}$

Question 14

Solve the system of equations by the substitution method.
-$$\begin{array} { l } 
y = 3 x + 9 \
y = 8 x + 8
\end{array}$$

Accepted Answer

A)  $\left\{ \left( \frac { 1 } { 5 } , \frac { 48 } { 5 } \right) \right\}$ 
B)  $\left\{ \left( \frac { 48 } { 5 } , \frac { 1 } { 5 } \right) \right\}$ 
C)  $\{ ( 1,12 ) \}$ 
D)  $\varnothing$ 
A)  $\left\{ \left( \frac { 1 } { 5 } , \frac { 48 } { 5 } \right) \right\}$ 
B)  $\left\{ \left( \frac { 48 } { 5 } , \frac { 1 } { 5 } \right) \right\}$ 
C)  $\{ ( 1,12 ) \}$ 
D)  $\varnothing$

Question 15

Graph the solution set of the system of inequalities or indicate that the system has no solution.
-$\begin{array}{l}
x+y \leq 7 \
y \geq 7 x-3 \
x \geq 0 \
y \geq 0
\end{array}$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 16

Solve the problem.
-A dietitian needs to purchase food for patients. She can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. The dietician is bound by the following constraints.
· Each ounce of chicken contains 13 grams of protein and 24 grams of carbohydrates.
· Each ounce of potatoes contains 5 grams of protein and 35 grams of carbohydrates.
· The minimum daily requirements for the patients under the dietitian's care are 45 grams of protein and
58 grams of carbohydrates.
Let x = the number of ounces of chicken and y = the number of ounces of potatoes purchased per patient.
Write a system of inequalities that describes these constraints.

Accepted Answer

A) 
$$\begin{array} { l } 
13 x + 5 y \geq 45 \
24 x + 35 y \geq 58
\end{array}$$ 
B) 
$$\begin{array} { r } 
13 x + 24 y \geq 45 \
5 x + 35 y \geq 58
\end{array}$$ 
C) 
$$13 x + 5 y \geq 58$$
$$24 x + 35 y \geq 45$$ 
D) 
$$\begin{array} { r } 
13 x + 24 x \geq 45 \
5 y + 35 y \geq 58
\end{array}$$ 
A) 
$$\begin{array} { l } 
13 x + 5 y \geq 45 \
24 x + 35 y \geq 58
\end{array}$$ 
B) 
$$\begin{array} { r } 
13 x + 24 y \geq 45 \
5 x + 35 y \geq 58
\end{array}$$ 
C) 
$$13 x + 5 y \geq 58$$
$$24 x + 35 y \geq 45$$ 
D) 
$$\begin{array} { r } 
13 x + 24 x \geq 45 \
5 y + 35 y \geq 58
\end{array}$$

Question 17

Solve the problem.
-A candy company has 130 pounds of cashews and 170 pounds of peanuts which they combine into two different mixes. The deluxe mix has half cashews and half peanuts and sells for $8 per pound. The
Economy mix has one third cashews and two thirds peanuts and sells for $5.90 per pound. How many
Pounds of each mix should be prepared for maximum revenue?

Accepted Answer

A) 180 pounds of deluxe and 120 pounds of economy 
B) 270 pounds of deluxe and 80 pounds of economy 
C) 90 pounds of deluxe and 40 pounds of economy 
D) 130 pounds of deluxe and 0 pounds of economy 
A) 180 pounds of deluxe and 120 pounds of economy 
B) 270 pounds of deluxe and 80 pounds of economy 
C) 90 pounds of deluxe and 40 pounds of economy 
D) 130 pounds of deluxe and 0 pounds of economy

Question 18

Solve the problem.
-The Jillson's have up to $75,000 to invest. They decide that they want to have at least $25,000 invested in
stable bonds yielding 6% and that no more than $45,000 should be invested in more volatile bonds
yielding 12%. How much should they invest in each type of bond to maximize income if the amount in the
more volatile bond should not exceed the amount in the more stable bond? What is the maximum income?

Accepted Answer

$37,500 in the stabl

Question 19

Solve Nonlinear Systems By Addition
Solve the system by the addition method.
-$$\begin{array} { l } 
x ^ { 2 } + y ^ { 2 } = 25 \
25 x ^ { 2 } + 9 y ^ { 2 } = 225
\end{array}$$

Accepted Answer

A)  $\{ ( 0,5 ) , ( 0 , - 5 ) \}$ 
B)  $\{ ( 5,0 ) , ( - 5,0 ) \}$ 
C)  $\{ ( 0,3 ) , ( 0 , - 3 ) \}$ 
D)  $\{ ( 3,0 ) , ( - 3,0 ) \}$ 
A)  $\{ ( 0,5 ) , ( 0 , - 5 ) \}$ 
B)  $\{ ( 5,0 ) , ( - 5,0 ) \}$ 
C)  $\{ ( 0,3 ) , ( 0 , - 3 ) \}$ 
D)  $\{ ( 3,0 ) , ( - 3,0 ) \}$

Question 20

An objective function and a system of linear inequalities representing constraints are given. Graph the system of
inequalities representing the constraints. Find the value of the objective function at each corner of the graphed
region. Use these values to determine the maximum value of the objective function and the values of x and y for
which the maximum occurs.
-$$\begin{array} { l l } 
\text { Objective Function } & \mathrm { z } = 3 \mathrm { x } + 5 \mathrm { y } \
\text { Constraints } & \mathrm { x } \geq 0 \
& \mathrm { y } \geq 0 \
& 2 x + y \leq 15 \
& x - 3 y \geq - 3
\end{array}$$

Accepted Answer

A) Maximum 33; at (6, 3) 
B) Maximum 75; at (0, 15) 
C) Maximum 22.5; at (7.5, 0) 
D) Maximum 38; at (6, 4) 
A) Maximum 33; at (6, 3) 
B) Maximum 75; at (0, 15) 
C) Maximum 22.5; at (7.5, 0) 
D) Maximum 38; at (6, 4)

Solve the system of equations by the substitution method. - y =5x+4 5y-15x =30

Solve the problem. -A right triangle has an area of 44 square inches. The square of the hypotenuse is 185. Find the lengths of the legs of the triangle. Round your answer to the nearest inch.

Graph the solution set of the system of inequalities or indicate that the system has no solution. - y lt;x+1 9x+10y gt;30 $Graph the solution set of the system of inequalities or indicate that the system has no solution. - \begin{array}{l} y<x+1 \\ 9 x+10 y>30 \end{array}$

Solve Nonlinear Systems By Addition Solve the system by the addition method. - 6+=36 6-=36

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. -Use the revenue and cost functions to write the profit function from producing and selling x binoculars.

Solve the system by the substitution method. - $x ^ { 2 } = y ^ { 2 } + 39$ $x - y = 3$

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. -Is there a profit when 947 binoculars are produced?

Graph the inequality. - $( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9$ $Graph the inequality. - ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9$

Solve the system of equations by the substitution method. - 5x-6y=2-5x 2x+6y=x+5y+-3

Solve the system of equations by the substitution method. - y=3x+9 y=8x+8

Solve Nonlinear Systems By Addition Solve the system by the addition method. - +=25 25+9=225

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Exponential and Logarithmic Functions

Matrices and Determinants

Conic Sections

Sequences, Induction, and Probability

Filters

Exam 5: Systems of Equations and Inequalities

Solve the system of equations by the substitution method. - y =5x+4 5y-15x =30

Solve the problem. -A right triangle has an area of 44 square inches. The square of the hypotenuse is 185. Find the lengths of the legs of the triangle. Round your answer to the nearest inch.

Graph the solution set of the system of inequalities or indicate that the system has no solution. - y lt;x+1 9x+10y gt;30

Solve Nonlinear Systems By Addition Solve the system by the addition method. - 6+=36 6-=36

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. -Use the revenue and cost functions to write the profit function from producing and selling x binoculars.

Solve the system by the substitution method. - x2=y2+39x ^ { 2 } = y ^ { 2 } + 39x2=y2+39 x−y=3x - y = 3x−y=3

The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. -Is there a profit when 947 binoculars are produced?

Graph the inequality. - (x+3)2+(y−4)2>9( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9(x+3)2+(y−4)2>9

Solve the system of equations by the substitution method. - 5x-6y=2-5x 2x+6y=x+5y+-3

Solve the system of equations by the substitution method. - y=3x+9 y=8x+8

Graph the solution set of the system of inequalities or indicate that the system has no solution. - x+y\leq7 y\geq7x-3 x\geq0 y\geq0

Solve Nonlinear Systems By Addition Solve the system by the addition method. - +=25 25+9=225

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Exponential and Logarithmic Functions

Matrices and Determinants

Conic Sections

Sequences, Induction, and Probability

Filters

Graph the solution set of the system of inequalities or indicate that the system has no solution. - y lt;x+1 9x+10y gt;30 $Graph the solution set of the system of inequalities or indicate that the system has no solution. - \begin{array}{l} y<x+1 \\ 9 x+10 y>30 \end{array}$

Solve the system by the substitution method. - $x ^ { 2 } = y ^ { 2 } + 39$ $x - y = 3$

Graph the inequality. - $( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9$ $Graph the inequality. - ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } > 9$