Exam 5: Systems of Equations and Inequalities
Exam 1: Equations and Inequalities420 Questions
Exam 2: Functions and Graphs83 Questions
Exam 3: Polynomial and Rational Functions98 Questions
Exam 4: Exponential and Logarithmic Functions268 Questions
Exam 5: Systems of Equations and Inequalities287 Questions
Exam 6: Matrices and Determinants152 Questions
Exam 7: Conic Sections120 Questions
Exam 8: Sequences, Induction, and Probability303 Questions
Select questions type
Solve the problem.
-Find the dimensions of a rectangle whose perimeter is 36 feet and whose area is 80 square feet.
(Multiple Choice)
4.8/5  (40)
(40)
Solve Problems Using Systems of Nonlinear Equations
Let x represent one number and let y represent the other number. Use the given conditions to write a system of
nonlinear equations. Solve the system and find the numbers.
-The difference between the squares of two numbers is 7. Twice the square of the second number subtracted from the square of the first number is -2. Find the numbers.
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-A coffee store has available 75 pounds of A grade coffee and 120 pounds of B grade coffee. These will be
blended into 1 pound packages as follows: an economy blend that contains 4 ounces of A grade coffee and
12 ounces of B grade coffee and a superior blend that contains 8 ounces of A grade coffee and 8 ounces of
B grade coffee. Using x to denote the number of packages of the economy blend and y to denote the
number of packages of the superior blend, write a system of linear inequalities that describes the possible
number of packages of each blend. Graph the system of inequalities. 
(Essay)
4.9/5  (45)
(45)
Solve the problem.
-In Miguel's home town, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing. The function y = 0.26x + 16.9 models the percentage, y, of women in this city
Who smoke x years after 1990. The function 0.20x + y = 27.3 models the percentage, y, of men in this city
Who smoke x years after 1990. Use these models to determine when the percentage of women who smoke
Will be the same as the percentage of men who smoke. Round to the nearest year. What percentage of
Women and what percentage of men (to the nearest whole percent)will smoke at that time?
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-You invested $6000 and started a business selling vases. Supplies cost $19 per vase and you are selling each vase for $29. Let x represent the number of vases produced and sold and write the cost function, C,
And revenue function, R.
(Multiple Choice)
4.7/5  (38)
(38)
Decompose P/Q, Where Q Has Repeated Linear Factors
Write the form of the partial fraction decomposition of the rational expression. It is not necessary to solve for the
constants.
-
(Multiple Choice)
5.0/5  (39)
(39)
Solve Nonlinear Systems By Addition
Solve the system by the addition method.
- y=+4 y=-+10
(Multiple Choice)
4.8/5  (36)
(36)
Determine whether the given ordered pair is a solution of the system.
- (2,5) 2x=9-y 3x=16-2y
(Multiple Choice)
4.9/5  (25)
(25)
Solve Problems Using Systems of Nonlinear Equations
Let x represent one number and let y represent the other number. Use the given conditions to write a system of
nonlinear equations. Solve the system and find the numbers.
-The sum of the squares of two numbers is 74. The sum of the two numbers is 12. Find the two numbers.
(Multiple Choice)
4.9/5  (42)
(42)
Solve the system of equations.
- x+y+z=10 x-y+3z=4 3x+y+z=16
(Multiple Choice)
4.9/5  (33)
(33)
Decompose P/Q, Where Q Has a Nonrepeated Prime Quadratic Factor
Write the form of the partial fraction decomposition of the rational expression. It is not necessary to solve for the
constants.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the system of equations by the substitution method.
- -4-2=22 =5
(Multiple Choice)
4.9/5  (27)
(27)
Determine if the given ordered triple is a solution of the system.
- (-2,5,-5) x+y+z=-2 x-y+5z=-32 2x+y+z=-4
(Multiple Choice)
4.8/5  (33)
(33)
Determine whether the given ordered pair is a solution of the system.
- (3,-2) x+y=1 x-y=5
(Multiple Choice)
4.8/5  (36)
(36)
Use Linear Programming to Solve Problems
Find the maximum or minimum value of the given objective function of a linear programming problem. The figure
illustrates the graph of the feasible points.
-Objective Function: z = 5x + 7y Find maximum and minimum. 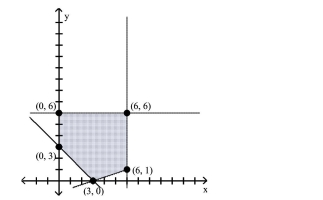
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A deli sells three sizes of chicken sandwiches: the small chicken sandwich contains 6 ounces of meat and sells for $2.50; the regular chicken sandwich contains 10 ounces of meat and sells for $3.00; and the large
Chicken sandwich contains 12 ounces of meat and sells for $3.50. A customer requests a selection of each
Size for a reception. She and the manager agree on a combination of 44 sandwiches made from 24 pounds
8 ounces of chicken for a total cost of $126. How many of each size sandwich will be in this combination?
(Note: 1 pound = 16 ounces)
(Multiple Choice)
4.8/5  (45)
(45)
Solve the system by the addition method.
- -6x+y=10 9x+4y=-4
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A ceramics workshop makes serving bowls, platters, and bread baskets to sell at its Winter Festival. A serving bowl takes 3 hours to prepare, 2 hours to paint, and 10 hours to fire. A platter takes 17 hours to
Prepare, 3 hours to paint, and 4 hours to fire. A bread basket takes 4 hours to prepare, 15 hours to paint,
And 7 hours to fire. If the workshop has 134 hours for prep time, 64 hours for painting, and 118 hours for
Firing, how many of each can be made?
(Multiple Choice)
4.9/5  (38)
(38)
Showing 101 - 120 of 287
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)