Exam 6: Discrete Probability Distributions
Exam 1: Basic Ideas39 Questions
Exam 2: Graphical Summaries of Data40 Questions
Exam 3: Numerical Summaries of Data76 Questions
Exam 4: Summarizing Bivariate Data33 Questions
Exam 5: Probability99 Questions
Exam 6: Discrete Probability Distributions76 Questions
Exam 7: The Normal Distribution131 Questions
Exam 8: Confidence Intervals62 Questions
Exam 9: Hypothesis Testing115 Questions
Exam 10: Two-Sample Confidence Intervals44 Questions
Exam 11: Two-Sample Hypothesis Tests43 Questions
Exam 12: Tests With Qualitative Data26 Questions
Exam 13: Inference in Linear Models51 Questions
Exam 14: Analysis of Variance48 Questions
Exam 15: Nonparametric Statistics27 Questions
Select questions type
Determine whether the random variable described is discrete or continuous. The total value of a set of coins
(Multiple Choice)
4.8/5  (36)
(36)
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 25% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 14 adult dogs is studied.
What is the standard deviation of the number of dogs who weigh 65 lb or more?
(Multiple Choice)
4.9/5  (26)
(26)
It is estimated that 40% of households own a riding lawn mower. A sample of 13 households is studied. What is the mean number of households who own a riding mower?
(Multiple Choice)
4.8/5  (38)
(38)
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 25% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 11 adult dogs is studied.
What is the mean number of dogs who weigh 65 lb or more?
(Multiple Choice)
4.8/5  (43)
(43)
At an airport, 83% of recent flights have arrived on time. A sample of 12 flights is studied. What is the standard deviation of the number of flights that are on time?
(Multiple Choice)
4.9/5  (36)
(36)
A sample of 6,000 computer monitors are examined for stuck pixels. Of them, 4,074 have no stuck pixels, 1,153 have one stuck pixel, 462 have two stuck pixels, 226 have three stuck pixels, and 85 Have four stuck pixels. Let X be the number of stuck pixels of a monitor randomly sampled from
This population. Find the probability distribution of X.
(Multiple Choice)
4.8/5  (45)
(45)
Determine the indicated probability for a binomial experiment with the given number of trials n and the given success probability p.
N = 11, p = 0.7, P(Fewer than 4)
(Multiple Choice)
4.9/5  (39)
(39)
Determine the indicated probability for a Poisson random variable with the given values of
(Multiple Choice)
4.8/5  (38)
(38)
An insurance company sells a one-year term life insurance policy to an 80-year-old woman. The woman pays a premium of $1000. If she dies within one year, the company will pay $18,500 to her Beneficiary. According to the company's statistics department, the probability that an 80-year-old Woman will be alive one year later is 0.9581. Find the expected value of the insurance company's Profit.
(Multiple Choice)
5.0/5  (31)
(31)
A survey asked 870 people how many times per week they dine out at a restaurant. The results are presented in the following table.
Number of Times Frequency 0 124 1 249 2 245 3 121 4 80 5 20 6 28 7 3 Total 870
Consider the 870 people to be a population. Let X be the number of times per week a person dines out For a person sampled at random from this population. Find the probability that a person dines out 4
Or more times per week.
(Multiple Choice)
4.9/5  (34)
(34)
Determine whether the table represents a discrete probability distribution.
x P(x) -1 0.4 0 0.3 1 0.1 2 0.35
(True/False)
5.0/5  (35)
(35)
Determine whether the random variable described is discrete or continuous. The length in seconds of a randomly-selected TV commercial
(Multiple Choice)
4.8/5  (34)
(34)
A student takes a true-false test that has 13 questions and guesses randomly at each answer. Let X be the number of questions answered correctly. Find P(Fewer than 4)
(Multiple Choice)
4.8/5  (36)
(36)
Last year, a manufacturer produced 1,950,000 DVD players. Of these, approximately 4% were defective. Assume that a simple random sample of n = 180 players is drawn. Use the Poisson Approximation to the binomial distribution to compute the probability that fewer than four of the 180 DVD players were defective.
(Multiple Choice)
4.9/5  (40)
(40)
The following table presents the probability distribution of the number of vacations X taken last year for a randomly chosen family. Compute the standard deviation
x 0 1 2 3 4 P(x) 0.11 0.69 0.13 0.05 0.02
(Multiple Choice)
5.0/5  (30)
(30)
The number of customers in a line at a supermarket express checkout counter is a random variable with the following probability distribution.
0 1 2 3 4 5 ( ) 0.10 0.25 0.30 0.18 0.07 0.10
Compute the mean
(Multiple Choice)
4.8/5  (37)
(37)
A survey asked 805 people how many times per week they dine out at a restaurant. The results are presented in the following table.
Number of Times Frequency 0 100 1 267 2 220 3 111 4 51 5 25 6 24 7 7 Total 805
Consider the 805 people to be a population. Let X be the number of times per week a person dines out For a person sampled at random from this population. Compute the standard deviation 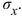
(Multiple Choice)
4.8/5  (24)
(24)
Last year, a manufacturer produced 200,000 DVD players. Of these, approximately 2% were defective. Assume that a simple random sample of n = 130 players is drawn. Use the Poisson Approximation to the binomial distribution to compute the mean number of DVD players that were Defective.
(Multiple Choice)
4.9/5  (36)
(36)
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 40% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 12 adult dogs is studied.
What is the probability that exactly 3 of them weigh 65 lb or more?
(Multiple Choice)
4.8/5  (40)
(40)
Fill in the missing value so that the following table represents a probability distribution.
x -4 -3 -2 -1 P(x) 0.19 0.28 ? 0.38
(Multiple Choice)
5.0/5  (36)
(36)
Showing 21 - 40 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)